136. Отрезок

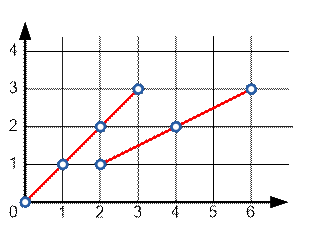
Задан отрезок, концы которого имеют целочисленные координаты. Подсчитайте количество точек отрезка, имеющих целочисленные координаты.

 

Вход. Четыре числа – координаты x1, y1, x2, y2 концов отрезка. Значения координат не превышают по модулю 2 * 109.

 

Выход. Выведите количество точек отрезка с целочисленными координатами.

 

Пример входа 1

Пример выхода 1

0 0 3 3

4

 

 

Пример входа 2

Пример выхода 2

2 1 6 3

3

 

 

РЕШЕНИЕ

НОД

 

Анализ алгоритма

Если (x1, y1) и (x2, y2) – целочисленные концы отрезка, то количество целочисленных точек на нем равно НОД ( |x2 – x1|, |y2 – y1| ) + 1.

Поскольку координаты концов отрезка по модулю не превышают 2 * 109, то модуль разности координат |x2 – x1| и |y2 – y1| не превышает 4 * 109. Например, если x1 = 2 * 109 и x2 = -2 * 109, то |x2 – x1| = 4 * 109. Поэтому при вычислениях следует воспользоваться 64 битовым целочисленным типом.

 

Пример

Для первого примера ответ равен

1 + НОД ( |3 – 0|, |3 – 0| ) = 1 + НОД (3, 3) = 1 + 3 = 4

Для второго примера ответ равен

1 + НОД ( |6 – 2|, |3 – 1| ) = 1 + НОД (4, 2) = 1 + 2 = 3

 

Реализация алгоритма

Функция gcd вычисляет наибольший общий делитель чисел a и b.

 

int gcd(int a, int b)

{

  return (!b) ? a : gcd(b,a % b);

}

 

Читаем входные данные.

 

scanf("%lld %lld %lld %lld",&x1,&y1,&x2,&y2);

 

Вычисляем ответ по формуле и выводим его.

 

res = gcd(abs(x2 - x1), abs(y2 - y1)) + 1;

printf("%lld\n",res);

 

Java реализация

 

public class Main

{

 

Функция gcd вычисляет наибольший общий делитель чисел a и b.

 

  static long gcd(long a, long b)

  {

    if (b == 0) return a;

    return gcd(b,a % b);

  }

 

  public static void main(String[] args)

  {

    Scanner con = new Scanner(System.in);

 

Читаем входные данные.

 

    long x1 = con.nextLong(),

         y1 = con.nextLong(),

         x2 = con.nextLong(),

         y2 = con.nextLong();

 

Вычисляем ответ по формуле и выводим его.

 

    long res = 1 + gcd(Math.abs(x2 - x1), Math.abs(y2 - y1));

    System.out.println(res);

  }

}

 

Python реализация

Функция gcd вычисляет наибольший общий делитель чисел a и b.

 

def gcd(a, b):

  if a == 0: return b

  if b == 0: return a

  if a > b: return gcd(a % b, b)

  return gcd(a, b % a)

 

Читаем входные данные.

 

x1, y1, x2, y2 = map(int, input().split())

 

Вычисляем ответ по формуле и выводим его.

 

res = gcd(abs(x2 - x1), abs(y2 - y1)) + 1

print(res)

 

Python реализация – gcd

Для вычисления НОД двух чисел воспользуемся функцией gcd, встроенной в языке Питон. 

 

import math

 

Читаем входные данные.

 

x1, y1, x2, y2 = map(int, input().split())

 

Вычисляем ответ по формуле и выводим его.

 

res = math.gcd(abs(x2 - x1), abs(y2 - y1)) + 1

print(res)