136. The segment

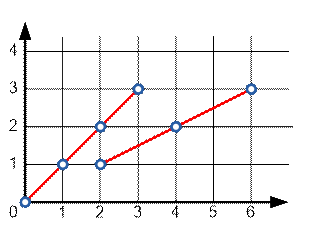
The endpoints of the segment have integer coordinates. Count the number of points on the segment with integer coordinates.

Input. Four integers represent the coordinates x₁, y₁, x₂, y₂ of the endpoints of the segment. The coordinate values do not exceed 2 * 10⁹ in absolute value.

Output. Print the number of points on the segment with integer coordinates.

Sample input 1	Sample output 1
0 0 3 3	4
Sample input 2	Sample output 2
2 1 6 3	3

SOLUTION

GCD

Algorithm analysis

If (x₁, y₁) and (x₂, y₂) are integer endpoints of the segment, then the number of integer points on it is equal to GCD ( |x₂ – x₁|, |y₂ – y₁| ) + 1.

Since the coordinates of the segment endpoints do not exceed 2 * 10⁹ in absolute value, the absolute difference of coordinates |x₂ – x₁| and |y₂ – y₁| does not exceed 4 * 10⁹. For example, if x₁ = 2 * 10⁹ and x₂ = -2 * 10⁹, then |x₂ – x₁| = 4 * 10⁹. Therefore, 64-bit integer type should be used for computations.

Example

For the first example, the answer is

1 + GCD ( |3 – 0|, |3 – 0| ) = 1 + GCD (3, 3) = 1 + 3 = 4

For the second example, the answer is

1 + GCD ( |6 – 2|, |3 – 1| ) = 1 + GCD (4, 2) = 1 + 2 = 3

Algorithm realization

The gcd function returns the greatest common divisor of the numbers a and b.

int gcd(int a, int b)

{

return (!b) ? a : gcd(b,a % b);

}

Read the input data.

scanf("%lld %lld %lld %lld",&x1,&y1,&x2,&y2);

Compute the answer using the formula and print it.

res = gcd(abs(x2 - x1), abs(y2 - y1)) + 1;

printf("%lld\n",res);

Java realization

import java.io.*;

import java.util.*;

public class Main

{

The gcd function returns the greatest common divisor of the numbers a and b.

static long gcd(long a, long b)

{

if (b == 0) return a;

return gcd(b,a % b);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

Read the input data.

long x1 = con.nextLong(),

y1 = con.nextLong(),

x2 = con.nextLong(),

y2 = con.nextLong();

Compute the answer using the formula and print it.

long res = 1 + gcd(Math.abs(x2 - x1), Math.abs(y2 - y1));

System.out.println(res);

}

}

Python realization

The gcd function returns the greatest common divisor of the numbers a and b.

def gcd(a, b):

if a == 0: return b

if b == 0: return a

if a > b: return gcd(a % b, b)

return gcd(a, b % a)

Read the input data.

x1, y1, x2, y2 = map(int, input().split())

Compute the answer using the formula and print it.

res = gcd(abs(x2 - x1), abs(y2 - y1)) + 1

print(res)

Python realization – gcd

To compute the greatest common divisor (GCD) of two numbers, let’s use the gcd function built into the Python language.

import math

Read the input data.

x1, y1, x2, y2 = map(int, input().split())

Compute the answer using the formula and print it.

res = math.gcd(abs(x2 - x1), abs(y2 - y1)) + 1

print(res)