137. НОД

Найдите наибольший общий делитель (НОД) n чисел.

Вход. Первая строка содержит количество чисел n (1 < n < 101). Вторая строка содержит n натуральных чисел, каждое из которых не превышает 30000.

Выход. Выведите одно число – НОД заданных чисел.

Пример входа	Пример выхода
2 15 25	5

РЕШЕНИЕ

НОД

Анализ алгоритма

Известно, что

НОД (a₁, a₂, …, a_i) = НОД (НОД (a₁, a₂, …, a_{i - 1}) , a_i)

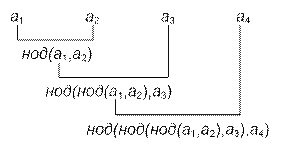
На этой основе можно последовательно вычислять наибольший общий делитель двух, трёх, …, n чисел. Например, для четырёх чисел выполняется равенство:

НОД (a₁, a₂, a₃, a₄) = НОД (НОД (НОД (НОД (0, a₁), a₂), a₃), a₄)

Реализация алгоритма

Функция gcd вычисляет наибольший общий делитель.

int gcd(int a, int b)

{

return (!b) ? a : gcd(b, a % b);

}

Читаем входные данные и в переменной res последовательно вычисляем НОД для заданных n чисел.

res = 0;

scanf("%d", &n);

while (n--)

{

scanf("%d", &b);

res = gcd(res, b);

}

Выводим ответ.

printf("%d\n", res);

Python реализация

import math

Читаем входные данные.

n = int(input())

lst = list(map(int,input().split()))

В переменной res последовательно вычисляем НОД для заданных n чисел

res = 0

for x in lst:

res = math.gcd(res, x)

Выводим ответ.

print(res)