145. Квадраты

Заданы длины n отрезков. Какое наибольшее количество квадратов можно из них составить? Сторона каждого квадрата должна состоять только из одного отрезка.

Вход. В первой строке находится количество отрезков n (1 ≤ n ≤ 10⁶). Во второй строке заданы n натуральных чисел – длины отрезков, числовые значения которых не превышают 100.

Выход. Выведите максимально возможное количество квадратов, которое можно составить из заданных отрезков.

Пример входа	Пример выхода
9 2 2 4 2 3 2 1 2 4	1

РЕШЕНИЕ

сортировка подсчетом

Анализ алгоритма

Пусть имеется k отрезков одинаковой длины. Тогда из них можно составить k / 4 квадрата. Длины отрезков изменяются от 1 до 100. Подсчитаем количество отрезков длины i (1 ≤ i ≤ 100) в cnt[i]. Тогда максимально возможное количество квадратов, которое можно составить из заданных отрезков, равно

cnt[1] / 4 + cnt[2] / 4 + …. + cnt[100] / 4

Пример

Рассмотрим состояние массива cnt после сортировки подсчетом.

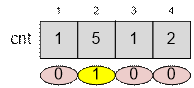
Из отрезков длины 2 можно составить 5 / 4 = 1 квадрат. Из остальных длин отрезков квадратов составить невозможно.

Реализация алгоритма

Объявим массив для подсчета.

int cnt[101];

Читаем входные данные. Совершаем сортировку подсчетом. В ячейке cnt[i] подсчитываем количество отрезков длины i.

scanf("%d",&n);

for(j = 0; j < n; j++)

{

scanf("%d",&i);

cnt[i]++;

}

В переменной res подсчитываем количество квадратов, которое можно построить.

res = 0;

for(i = 1; i <= 100; i++)

res += cnt[i] / 4;

Выводим ответ.

printf("%d\n",res);

Java реализация

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int cnt[] = new int[101];

for(int i = 0; i < n; i++)

{

int val = con.nextInt();

cnt[val]++;

}

int res = 0;

for(int i = 1; i <= 100; i++)

res += cnt[i] / 4;

System.out.println(res);

con.close();

}

}