1910. Империя

Империя включает в себя n планет. Пронумеруем эти планеты числами от 1 до n. Планета с номером 1 – столица Империи, где находится резиденция Императора и подготавливаются войска. На различных планетах империи часто вспыхивают восстания, которые приходится подавлять военной силой и немедленно.

Для того чтобы войска могли быстро передвигаться, на некоторых планетах установлены односторонние телепорты. Всего телепортов m штук. С помощью i-ого телепорта можно в мгновение ока попасть с планеты a_i на планету b_i (но не наоборот). Таким образом, вовремя подавить восстание на некоторой планете x можно, если существует последовательность планет p₁, ..., p_k (k ≥ 2) такая, что p₁ = 1, p_k = x, а для каждого 1 ≤ i < k есть телепорт из планеты с номером p_i на планету с номером p_i+1. Учитывая, что после подавления восстания войска остаются на планете для поддержания порядка, об их возвращении в столицу мы можем не беспокоиться.

Проверьте, есть ли возможность при имеющихся телепортах подавить восстание на любой планете Империи. Если это так, то выведите 0. В противном случае, найдите наименьшее количество телепортов, которое надо дополнительно построить, чтобы восстание на любой планете было подавляемо. Каждый телепорт может быть построен между произвольными двумя планетами.

Вход. Первая строка содержит два целых числа n и m (2 ≤ n ≤ 10⁵, 0 ≤ m ≤ 2·10⁵). i-ая из следующих m строк содержит пару чисел a_i, b_i (1 ≤ a_i, b_i ≤ n) для всех 1 ≤ i ≤ m. Ни на одной планете нет телепорта в саму себя. Ни на одной планете нет двух телепортов на одну и ту же планету.

Выход. Выведите наименьшее количество телепортов, гарантирующее, что восстание на любой планете можно будет немедленно подавить.

Пример входа	Пример выхода
6 4 3 1 4 6 1 2 4 5	2

РЕШЕНИЕ

графы – сильная связность

Анализ алгоритма

В графе, представляющем империю, требуется добавить наименьшее количество ребер так, чтобы любая вершина была достижимой из вершины 1 (столицы).

Заметим, что новые дуги можно проводить только из первой вершины. Действительно, если новой дугой будет (a, b), то заменив ее на (1, b), мы не изменим достижимость вершин из столицы.

Рассмотрим конденсацию графа и выберем в ней вершину, в которую не входят ребра (граф конденсации ацикличен, такие вершины всегда существуют). Этой вершине соответствует некоторая сильно связная компонента. Из вершины 1 необходимо провести дугу в одну из вершин этой сильно связной компоненты. Здесь имеется одно исключение – если вершина 1 входит сама в эту сильно связную компоненту, тогда дуги проводить не надо.

Если в графе конденсации в вершину v входят ребра, то новых ребер в исходном графе из вершины 1 в вершины сильно связной компоненты, соответствующей v, проводить не надо.

Таким образом, в задаче следует найти количество сильно связных компонент, в которые в графе конденсации не ведут ребра. Отдельно следует обработать компоненту, в которую входит столица.

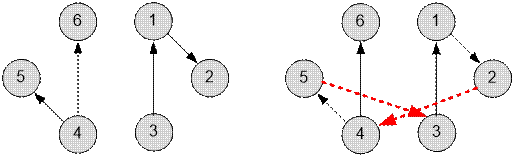
Пример

Граф, приведенный в примере, имеет следующий вид:

Для решения задачи достаточно построить два дополнительных телепорта. Можно, например, построить телепорт из планеты 2 на планету 4 и из планеты 5 на планету 3.

Указанный граф имеет 6 сильно связных компонент: каждая вершина является отдельной компонентой. Находим компоненты, в которые не ведут ребра. Таковых будет две: те, которые содержат вершины 3 и 4.

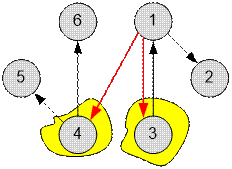
Таким образом достаточно построить из столицы (вершины 1) два новых телепорта, ведущих соответственно в вершины 3 и 4.

Реализация алгоритма

Империю будем представлять в виде графа и хранить в виде списка смежности g. Транспонированный граф храним в массиве gr. Массив used используется для отмечания уже пройденных вершин, top для топологической сортировки вершин, а color для покраски вершин согласно их вхождению в компоненты сильной связности.

vector<vector<int> > g, gr;

vector<int> used, top, color;

Функция dfs1 совершает поиск в глубину на входном графе. В массив top заносим вершины графа в такой последовательности, в которой поиск в глубину завершает их обработку.

void dfs1(int v)

{

used[v] = 1;

for (int to : g[v])

if (!used[to]) dfs1(to);

top.push_back(v);

}

Функция dfs2 совершает поиск в глубину на транспонированном графе. Все вершины компоненты сильной связности, в которую входит v, красим цветом c.

void dfs2(int v, int c)

{

color[v] = c;

for (int to : gr[v])

if (color[to] == -1) dfs2(to, c);

}

Основная часть программы. Читаем входные данные и строим граф империи g. Одновременно строим транспонированный граф gr.

scanf("%d %d",&n,&m);

g.resize(n+1);

gr.resize(n+1);

for(i = 0; i < m; i++)

{

scanf("%d %d",&a,&b);

g[a].push_back(b);

gr[b].push_back(a);

}

Запускаем первый обход в глубину на графе. Топологически сортируем вершины графа в массиве top.

used.resize(n+1);

for(i = 1; i <= n; i++)

if (!used[i]) dfs1(i);

Произведем покраску вершин. Вершины, входящие в одну компоненту сильной связности, красим одним и тем же цветом. Текущий цвет раскраски находится в переменной с.

color.assign(n+1,-1);

c = 0;

for(i = 1; i <= n; i++)

{

v = top[n-i];

if (color[v] == -1) dfs2(v,c++);

}

Значение с равно количеству компонент сильной связности, равное количеству вершин в конденсации графа. Вычислим количество компонент, в которые не ведут ребра в графе конденсации. Положим used[c] = 0, если в вершины, покрашенные цветом с, не требуется проводить нового ребра из столицы. Такой цвет с будет называть бесполезным.

used.assign(c,1);

for(i = 1; i < g.size(); i++)

for (int to : g[i])

Для каждого ребра (i, to) проверяем, лежат ли вершины i и to в разных компонентах сильной связности. Если это так, то объявим цвет color[to] бесполезным.

if (color[i] != color[to]) used[color[to]] = 0;

Проводить ребро из первой вершины (столицы) в вершину компоненты связности, в которой находится столица, не надо. Поэтому отметим цвет столицы как бесполезный (даже если возможно он уже таковым был отмечен раньше).

used[color[1]] = 0;

Вычисляем и выводим количество компонент сильной связности, в которые в графе конденсации не ведут ребра.

c = 0;

for(i = 0; i < used.size(); i++)

if (used[i]) c++;

Выводим ответ.

printf("%d\n",c);

Java реализация

import java.util.*;

public class Main

{

static ArrayList<Integer>[] g, gr;

static int used[], color[];

static Vector<Integer> top = new Vector<Integer>();

static void dfs1(int v)

{

used[v] = 1;

for(int i = 0; i < g[v].size(); i++)

{

int to = g[v].get(i);

if (used[to] == 0) dfs1(to);

}

top.add(v);

}

static void dfs2(int v, int c)

{

color[v] = c;

for(int i = 0; i < gr[v].size(); i++)

{

int to = gr[v].get(i);

if (color[to] == -1) dfs2(to,c);

}

}

@SuppressWarnings("unchecked")

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int m = con.nextInt();

g = new ArrayList[n+1];

for(int i = 0; i <= n; i++)

g[i] = new ArrayList<Integer>();

gr = new ArrayList[n+1];

for(int i = 0; i <= n; i++)

gr[i] = new ArrayList<Integer>();

for (int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g[a].add(b);

gr[b].add(a);

}

used = new int[n+1];

for(int i = 1; i <= n; i++)

if (used[i] == 0) dfs1(i);

color = new int[n+1];

Arrays.fill(color, -1);

int c = 0;

for(int i = 1; i <= n; i++)

{

int v = top.get(n-i);

if (color[v] == -1) dfs2(v,c++);

}

used = new int[c];

Arrays.fill(used, 1);

for(int i = 1; i < g.length; i++)

for(int j = 0; j < g[i].size(); j++)

{

int to = g[i].get(j);

// check edge i -> j if they in the same scc.

if (color[i] != color[to]) used[color[to]] = 0;

}

used[color[1]] = 0;

c = 0;

for(int i = 0; i < used.length; i++)

if (used[i] == 1) c++;

System.out.println(c);

con.close();

}

}