1910. Empire

The Empire consists of n planets. Lets label these planets with numbers from 1 to n. The planet with the number 1 is a capital of Empire, where the Emperor residence is located and the troops are prepared. On different planets of the empire the uprisings are often, which must be suppressed by force and immediately.

In order for troops to move quickly, the one-way teleports are installed on some planets. There are m teleports in total. Using the i-th teleport you can get instantly from planet a_i to planet b_i (but not vice versa). Thus, it is possible to crush the rebellion in time on some planet x, if there is a sequence of planets p₁, ..., p_k (k ≥ 2) such that p₁ = 1, p_k = x, and for each 1 ≤ i < k there is a teleport from planet with number p_i to the planet with number p_i+1. After crushing the uprising, the troops remain on the planet to maintain the order, so we do not need to worry about their return to the capital.

Check is there an opportunity using the existing system of teleports to crush the rebellion on any planet of the Empire. If so, print 0. Otherwise find the minimum number of teleports that must be built more so that the rebellion on any planet can be suppressed instantly. Each new teleport can be constructed between any two planets.

Input. The first line contains two integers n and m (2 ≤ n ≤ 10⁵, 0 ≤ m ≤ 2·10⁵). The i-th of the next m lines contains the pair of numbers a_i, b_i (1 ≤ a_i, b_i ≤ n) for all 1 ≤ i ≤ m. No one planet has a teleport to itself. No one planet has two teleports to the same planet.

Output. Print the minimum number of teleports, ensuring that the revolt on any planet can be immediately suppressed.

Sample input	Sample output
6 4 3 1 4 6 1 2 4 5	2

SOLUTION

graphs – strong connected components

Algorithm analysis

In the graph representing the empire, add the least number of edges so that any vertex is reachable from vertex 1 (the capital).

Note that new edges can only be constructed from the first vertex. Indeed, if the new arc is (a, b), then replacing it with (1, b), we will not change the reachability of the vertices from the capital.

Consider a graph condensation and choose a vertex that does not have incoming edges (the condensation graph is acyclic, such vertices always exist). Some strongly connected component corresponds to this vertex. From vertex 1 it is necessary to construct an edge to one of the vertices of this strongly connected component. There is one exception here – if vertex 1 itself is included in this strongly connected component, then no edge need to be constructed.

If in the condensation graph there are edges incoming to the vertex v, then there is no need to construct new edges in the original graph from vertex 1 to the vertices of the strongly connected component corresponding to v.

Thus, in this problem it is necessary to find the number of strongly connected components into which there is no incoming edges in condensation graph. The component that contains the capital should be processed separately.

Example

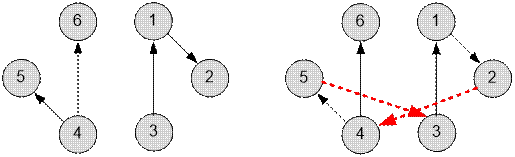
Graph given in a sample, has the form:

To solve the problem, it is enough to build two additional teleports. You can, for example, build a teleport from planet 2 to planet 4 and from planet 5 to planet 3.

The given graph has 6 strongly connected components: each vertex forms a separate component. Find the components without incoming edges. There will be two of them: those that contain vertices 3 and 4.

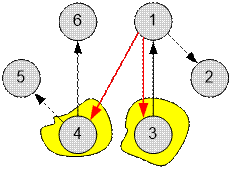
Thus, it is enough to build two new teleports from the capital (vertex 1), running respectively to vertices 3 and 4.

Algorithm realization

Represent the empire as a graph and store it in an adjacency list g. Store the transposed graph in the adjacency list gr. The array used is used to mark the already visited vertices, top for topological sorting of the vertices, and color for coloring the vertices according to their occurrence in the strongly connected components.

vector<vector<int> > g, gr;

vector<int> used, top, color;

The function dfs1 implements depth first search on the input graph. In the array top store the vertices in the order in which the depth first search ends their processing.

void dfs1(int v)

{

used[v] = 1;

for (int to : g[v])

if (!used[to]) dfs1(to);

top.push_back(v);

}

The function dfs2 implements depth first search on the reversed graph. Color all the vertices of the strongly connected component that contains v with color c.

void dfs2(int v, int c)

{

color[v] = c;

for (int to : gr[v])

if (color[to] == -1) dfs2(to, c);

}

The main part of the program. Read the input data and build the graph of empire g. Simultaneously construct the reversed graph gr.

scanf("%d %d",&n,&m);

g.resize(n+1);

gr.resize(n+1);

for(i = 0; i < m; i++)

{

scanf("%d %d",&a,&b);

g[a].push_back(b);

gr[b].push_back(a);

}

Start the first depth first search on the graph. Sort topologically the vertices of the graph in the array top.

used.resize(n+1);

for(i = 1; i <= n; i++)

if (!used[i]) dfs1(i);

Color the vertices. The vertices included in one strongly connected component are colored with the same color. The current color is in the variable c.

color.assign(n+1,-1);

c = 0;

for(i = 1; i <= n; i++)

{

v = top[n-i];

if (color[v] == -1) dfs2(v,c++);

}

The value of c equals to the number of strongly connected components and equals to the number of vertices in the condensation of the graph. Compute the number of connected components without incoming edges in the condensation graph. Set used[c] = 0, if it is not required to create a new edge from the capital to the vertices colored with color c. Such color с will be called useless.

used.assign(c,1);

for(i = 1; i < g.size(); i++)

for (int to : g[i])

For each edge (i, to), check whether the vertices i and to are in different strongly connected components. If so, then declare color color[to] as useless.

if (color[i] != color[to]) used[color[to]] = 0;

There is no need to create an edge from the first vertex (capital) to the vertex of the connected component where the capital is located. Therefore, let’s mark the color of the capital as useless (even if it may have already been marked as such before).

used[color[1]] = 0;

Compute and print the number of strongly connected components without incoming edges in the condensation graph.

c = 0;

for(i = 0; i < used.size(); i++)

if (used[i]) c++;

Print the answer.

printf("%d\n",c);

Java realization

import java.util.*;

public class Main

{

static ArrayList<Integer>[] g, gr;

static int used[], color[];

static Vector<Integer> top = new Vector<Integer>();

static void dfs1(int v)

{

used[v] = 1;

for(int i = 0; i < g[v].size(); i++)

{

int to = g[v].get(i);

if (used[to] == 0) dfs1(to);

}

top.add(v);

}

static void dfs2(int v, int c)

{

color[v] = c;

for(int i = 0; i < gr[v].size(); i++)

{

int to = gr[v].get(i);

if (color[to] == -1) dfs2(to,c);

}

}

@SuppressWarnings("unchecked")

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int m = con.nextInt();

g = new ArrayList[n+1];

for(int i = 0; i <= n; i++)

g[i] = new ArrayList<Integer>();

gr = new ArrayList[n+1];

for(int i = 0; i <= n; i++)

gr[i] = new ArrayList<Integer>();

for (int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g[a].add(b);

gr[b].add(a);

}

used = new int[n+1];

for(int i = 1; i <= n; i++)

if (used[i] == 0) dfs1(i);

color = new int[n+1];

Arrays.fill(color, -1);

int c = 0;

for(int i = 1; i <= n; i++)

{

int v = top.get(n-i);

if (color[v] == -1) dfs2(v,c++);

}

used = new int[c];

Arrays.fill(used, 1);

for(int i = 1; i < g.length; i++)

for(int j = 0; j < g[i].size(); j++)

{

int to = g[i].get(j);

// check edge i -> j if they in the same scc.

if (color[i] != color[to]) used[color[to]] = 0;

}

used[color[1]] = 0;

c = 0;

for(int i = 0; i < used.length; i++)

if (used[i] == 1) c++;

System.out.println(c);

con.close();

}

}