1934. Граф операций
Задан
неориентированный граф. Каждому ребру (u,
v) графа приписана некоторая бинарная
операция и некоторое число c. Число c
может принимать значения 0 или 1, а операции могут быть следующими: логическое
умножение (AND), логическое сложение (OR) и сложение по модулю два (XOR).
Необходимо выяснить, можно ли присвоить каждой вершине u число 0 или 1 (обозначим это значение как A(u)) таким образом, чтобы для каждого ребра (u, v) результат
приписанной ему бинарной операции над величинами A(u) и A(v) был равен
написанному на нем числу c.
Правила
вычисления указанных операций:
·
(0 AND 1) = (1
AND 0) = (0
AND 0) = 0,
(1 AND
1) = 1
·
(0 OR 1) = (1 OR
0) =
(1 OR 1) =
1, (0 OR 0) = 0
·
(0 XOR 1) = (1
XOR 0) = 1,
(1 XOR 1) =
(0 XOR
0) = 0
Вход. В первой строке записано количество вершин n и ребер m в графе (1 ≤ n
≤ 1000, 0 ≤ m ≤
300000). Следующие m строк содержат
описание ребер. Ребро задается номерами соединяемых вершин ui, vi
(1 ≤ ui, vi ≤ n, ui
≠ vi), числом ci и названием операции (AND,
OR или XOR). Никакое ребро не задается более одного раза.
Выход. Выведите
"YES", если можно найти требуемый набор значений для вершин, и
"NO" в противном случае.
|
Пример
входа |
Пример
выхода |
3 31 2 1 OR2 3 1 AND
1 3 1 XOR |
YES |
РЕШЕНИЕ
графы –
2-выполнимовсть
Анализ алгоритма
Запишем бинарную
операцию для каждого ребра в виде конъюнктивной нормальной формы, где каждый
конъюнкт содержит в точности 2 дизъюнкта. Для этого выразим бинарные операции в
импликативной форме.
u OR v = 1. Эквивалентно !u É v;
u OR v = 0. Эквивалентно (u É !u) AND (v É !v);
u AND v = 1. Эквивалентно (!u É u) AND (!v É v);
u AND v = 0. Эквивалентно !u OR !v = 1 или (u É !v) ;
Известно, что u XOR v = (u OR v)
AND (!u OR !v) = (!u É v) AND (u É !v).
u XOR v = 1. Эквивалентно (!u É v) AND (u É !v)
u XOR v = 0. Эквивалентно (u É v) AND (v É u);
Строим граф импликаций и решаем задачу
2-выполнимости за полиномиальное время.
Пример
Граф, приведенный в примере, имеет
следующий вид:

Требуемый набор
значений для вершин существует. Вершине v1
можно присвоить значение 0, вершине v2
значение 1, а вершине v3
значение 1. Тогда выполняются все три бинарные операции:
·
ребро (1, 2): 0 OR 1 = 1,
·
ребро (2, 3): 1 AND 1 = 1,
·
ребро (1, 3): 0 XOR 1 = 1
Построим граф
импликаций. Расщепим вершину v1
на 0 (соответствует v1) и
1 (соответствует !v1),
вершину v2 на 2 и 3
(соответствуют v2 и !v2), вершину v3 на 4 и 5 (соответствуют v3 и !v3).
Построим ребра:
·
v1 OR v2 = 1 эквивалентно !v1 É v2. Добавляем ребра (!v1, v2)
и (!v2, v1),
·
v2 AND v3 = 1 эквивалентно (!v2 É v2) AND (!v3
É v3). Добавляем ребра (!v2, v2) и (!v3,
v3),
·
v1 XOR v3 = 1 эквивалентно (!v1 É v3) AND (v3
É !v1). Добавляем ребра (!v1, v3), (!v3,
v1) и (v3, !v1), (v1,
!v3).
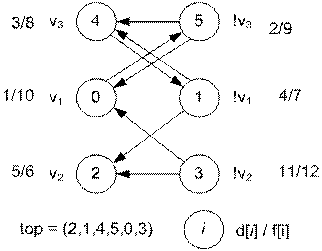
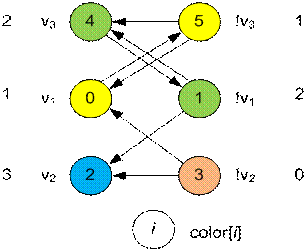
Вершины,
входящие в одну компоненту сильной связности, имеют одинаковый цвет. Сбоку от
вершины i записан ее цвет color[i]. Заметим, что для любого ребра (u, v),
принадлежащего конденсации графа, имеет место неравенство color[u] < color[v]. Выберем вершинам vi
значения.
1 = color[v1] < color[!v1]
= 2, выбираем A(v1) = 0;
2 = color[v2] > color[!v2]
= 0, выбираем A(v2) = 1;
2 = color[v3] > color[!v3]
= 1, выбираем A(v3) = 1;
Реализация алгоритма
Входной граф
храним в списке смежности g. Обратный граф (граф, в котором изменены все
направления ребер) храним списке смежности gr. Массив used используется для
отмечания уже пройденных вершин, top для топологической сортировки вершин, а
Color для покраски вершин согласно их вхождению в компоненты сильной связности.
vector<vector<int> > g, gr;
vector<int> used, top, Color;
Поиск в глубину
на входном графе. В массив top заносим последовательность вершин, в которой
поиск в глубину завершает их обработку.
void dfs1(int
v)
{
int i, to;
used[v] = 1;
for(i = 0; i
< g[v].size(); i++)
{
to = g[v][i];
if
(!used[to]) dfs1(to);
}
top.push_back(v);
}
Поиск в глубину на обратном графе.
Все вершины, которые будут пройдены в результате рекурсивного вызова функции
dfs2, принадлежат одной компоненте сильной связности. Красим все пройденные
вершины цветом с.
void dfs2(int
v, int c)
{
int i, to;
Color[v] = c;
for(i = 0; i
< gr[v].size(); i++)
{
to = gr[v][i];
if
(Color[to] == -1) dfs2(to,c);
}
}
Согласно импликативной связи u É v добавляем в
граф ребра (u, v) и (!v, !u).
void AddEdge(int
u, int v)
{
g[u].push_back(v); g[v^1].push_back(u^1);
gr[v].push_back(u); gr[u^1].push_back(v^1);
}
Основная часть
программы. Вершины входного графа нумеруются от 1 до n. Поскольку каждую вершину входного графа следует расщепить на
две, то поставим в соответствие вершине vi
входного графа вершины 2i – 2 и 2i – 1 в графе импликаций. Вершины графа импликаций
будут нумероваться с 0 до 2n – 1,
причем четным вершинам будут соответствовать вершины vi, а нечетным их отрицания !vi.
scanf("%d %d",&n,&m);
g.assign(2*n,0);gr.assign(2*n,0);
for(i = 0; i < m; i++)
{
scanf("%d %d
%d %s\n",&u,&v,&value,command);
u = 2 * u - 2; v = 2 * v - 2;
Строим ребра графа импликаций для операции OR. Если u OR v = 1, то
добавляем ребро (!u, v). При u OR v = 0 добавляем
ребра (u, !u) и (v, !v).
if
(command[0] == 'O')
{
if (value
== 1) AddEdge(u^1, v);
else
{
AddEdge(u, u^1);
AddEdge(v, v^1);
}
}
Строим ребра графа импликаций для операции AND. Если u AND v = 0, то
добавляем ребро (u, !v). При u AND v = 1 добавляем ребра
(!u, u) и (!v, v).
if
(command[0] == 'A')
{
if (value
== 0) AddEdge(u, v^1);
else
{
AddEdge(u^1, u);
AddEdge(v^1, v);
}
}
Строим ребра графа импликаций для операции XOR. Если u XOR v = 0, то
добавляем ребра (u, v) и (v, u). При u XOR v = 1 добавляем ребра (!u,
v) и (u, !v).
if
(command[0] == 'X')
{
if (value
== 1)
{
AddEdge(u, v^1);
AddEdge(u^1, v);
}
else
{
AddEdge(u, v);
AddEdge(v, u);
}
}
}
Запускаем поиск в глубину на графе
импликаций. Последовательность, в которой завершается обработка вершин графа,
сохраняется в массиве top.
used.assign(2*n,0);
for(i = 0; i < 2*n; i++)
if (!used[i])
dfs1(i);
Запускаем поиск в глубину на обратном
графе. Вершины обратного графа рассматриваем в порядке обхода массива top с
конца в начало. Вершины, входящие в одну компоненту сильной связности, красим
одним и тем же цветом. Текущий цвет раскраски находится в переменной с.
Color.assign(2*n,-1);
for(i = 0, c = 0; i < 2*n; i++)
{
v = top[2*n-i-1];
if (Color[v]
== -1) dfs2(v,c++);
}
Если некоторая переменная и ее
отрицание входят в одну сильно связную компоненту (соответствующие ей вершины i и i
XOR 1 покрашены одним цветом), то решения не существует.
for (flag = i = 0; i < 2*n; i += 2)
if (Color[i]
== Color[i^1])
{
flag = 1; break;
}
В зависимости от значения flag выводим ответ.
printf("%s\n", flag
? "NO" : "YES");