1937. Противопожарная безопасность

В городе Зеленоград n домов. Некоторые из них соединены дорогами с односторонним движением.

В последнее время в Зеленограде участились случаи пожаров. В связи с этим жители решили построить в городе несколько пожарных станций. Но возникла проблема — едущая по вызову пожарная машина, конечно, может игнорировать направление движения текущей дороги, однако, возвращающаяся с задания машина обязана следовать правилам дорожного движения (жители Зеленограда свято чтут эти правила!).

Ясно, что где бы ни оказалась пожарная машина, у неё должна быть возможность вернуться на ту пожарную станцию, с которой выехала. Но строительство станций стоит больших денег, поэтому на совете города было решено построить минимальное количество станций таким образом, чтобы это условие выполнялось. Кроме того, для экономии было решено строить станции в виде пристроек к уже существующим домам.

Ваша задача – написать программу, рассчитывающую оптимальное положение станций.

Вход. В первой строке задано число домов n (1 ≤ n ≤ 3000). Во второй строке записано количество дорог m (1 ≤ m ≤ 10⁵). Далее следует описание дорог в формате a_i b_i, означающее, что по i-й дороге разрешается движение автотранспорта от дома a_i к дому b_i (1 ≤ a_i, b_i ≤ n).

Выход. В первой строке выведите минимальное количество пожарных станций k, которые необходимо построить. Во второй строке выведите k чисел в произвольном порядке – дома, к которым необходимо пристроить станции. Если оптимальных решений несколько, выведите любое.

Пример входа	Пример выхода
5 7 1 2 2 3 3 1 2 1 2 3 3 4 2 5	2 4 5

РЕШЕНИЕ

графы – сильная связность

Анализ алгоритма

В задаче требуется найти минимальное множество вершин, достижимое из всех остальных в графе. Найдем конденсацию графа. Рассмотрим компоненту сильной связности, из которой не выходит ни одного ребра. Если ни в одной из ее вершин не построить пожарной станции, то пожарная машина, приехав из другой компоненты, сможет потушить пожар, но добраться домой следуя направлению дорог уже не сможет. Поэтому если из некоторой компоненты нет исходящих ребер, то в ней обязательно надо построить пожарную станцию. Других станций строить не надо, так как из любой вершины всегда можно попасть по ребрам графа в компоненту без исходящих из нее ребер.

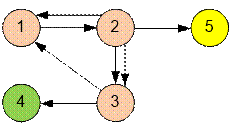
Пример

Входной граф содержит три сильно связные компоненты. Из компонент, состоящих из одной вершины (4 и 5), не исходит ни одно ребро. Следовательно достаточно именно в них строить пожарные станции.

Реализация алгоритма

Входной граф храним в списке смежности g. Обратный граф (граф, в котором изменены все направления ребер) храним списке смежности gr.

vector<vector<int> > g, gr;

vector<int> used, top, color, repr;

Функция dfs1 реализует  поиск  в глубину на входном графе. В массив top заносим последовательность вершин, в которой поиск в глубину завершает их обработку.

void dfs1(int v)

{

used[v] = 1;

for (int to : g[v])

if (!used[to]) dfs1(to);

top.push_back(v);

}

Функция dfs2 реализует  поиск в глубину на обратном графе. Все вершины, которые будут пройдены в результате рекурсивного вызова функции dfs2, принадлежат одной компоненте сильной связности. Красим все пройденные вершины цветом с. Вершины, находящиеся в одной сильно связной компоненте, имеют одинаковый цвет. Для каждого цвета с запомним в массиве repr ее представителя – любой номер вершины, покрашенной цветом с.

void dfs2(int v, int c)

{

color[v] = c;

repr[c] = v;

for (int to : gr[v])

if (color[to] == -1) dfs2(to, c);

}

Основная часть программы. Читаем входные данные. Строим обратный граф.

scanf("%d %d", &n, &m);

g.resize(n + 1);

gr.resize(n + 1);

for(i = 0; i < m; i++)

{

scanf("%d %d", &a, &b);

g[a].push_back(b);

gr[b].push_back(a);

}

Запускаем поиск в глубину на входном графе. Последовательность, в которой завершается обработка вершин графа, сохраняется в массиве top.

used.resize(n+1);

for(i = 1; i <= n; i++)

if (!used[i]) dfs1(i);

Запускаем поиск в глубину на обратном графе. Вершины обратного графа рассматриваем в порядке обхода массива top справа налево (с конца в начало). Для удобства дальнейшей обработки обернем массив top.

color.assign(n+1, -1);

repr.assign(n+1, -1);

reverse(top.begin(), top.end());

Вершины, входящие в одну компоненту сильной связности, красим одним и тем же цветом. Текущий цвет раскраски находится в переменной с.

c = 0;

for (int v : top)

if (color[v] == -1) dfs2(v, c++);

Переменная c содержит количество компонент связности.

used.assign(c, 1);

for(i = 1; i < g.size(); i++)

for (int to : g[i])

Перебираем все ребра графа (i, to). Проверяем, лежат ли вершины i и to в разных сильно связных компонентах. Это так, если они покрашены разными цветами. В этом случае нет смысла строить пожарную станцию в компоненте связности цвета color[i], поэтому установим used[color[i]] = 0.

if (color[i] != color[to]) used[color[i]] = 0;

}

Подсчитаем количество компонент c, в которых следует построить пожарную станцию.

c = 0;

for(i = 0; i < used.size(); i++)

if (used[i]) c++;

Выводим количество пожарных станций c, которое необходимо построить.

printf("%d\n",c);

Для каждой компоненты цвета i, из которой не выходят ребра, выведем по одному ее представителю (значение repr[i]) – это и будут номера домов, возле которых следует построить пожарные станции.

for(i = 0; i < used.size(); i++)

if (used[i]) printf("%d ",repr[i]);

printf("\n");