1937. Fire safety

In city X, there are n houses. Some of them are connected by one-way roads.

Recently, the number of fires in city X has increased. To address this problem, the residents decided to build several fire stations in the city. However, a difficulty arose: when responding to an emergency, a fire truck may ignore the direction of the roads, but on the way back it must strictly follow all traffic rules (the residents of city X observe them rigorously!).

It is necessary to ensure that, regardless of its current location, a fire truck can always return to the same fire station from which it departed. Since building fire stations is costly, the city council decided to construct the minimum possible number of stations that satisfy this condition. In addition, in order to reduce costs, fire stations may only be built next to existing houses.

Write a program that determines the optimal placement of fire stations.

Input. The first line contains the number of houses n (1 ≤ n ≤ 3000).

The second line contains the number of roads m (1 ≤ m ≤ 10⁵).

Each of the following  lines describes a road in the format a_i b_i, which means that it is possible to travel along the i-th road from house a_i to house b_i (1 ≤ a_i, b_i ≤ n).

Output. In the first line, print the minimum number k of fire stations that need to be built. In the second line, print k integers in any order – the indices of the houses next to which the fire stations should be built.

If there are multiple optimal solutions, print any of them.

Sample input	Sample output
5 7 1 2 2 3 3 1 2 1 2 3 3 4 2 5	2 4 5

SOLUTION

graphs – strongly connected components

Algorithm analysis

The problem requires finding a minimum set of vertices of the graph that is reachable from all other vertices. To do this, we consider the condensation of the graph. Let us focus on the strongly connected components from which no edges leave.

If a fire station is not built in such a component, a fire truck arriving from another component will be able to extinguish the fire, but it will not be able to return back while following the directions of the roads. Therefore, in each strongly connected component with no outgoing edges, at least one fire station must be built.

There is no need to build additional stations, since from any vertex of the graph there exists a path along the edges to one of the components with no outgoing edges.

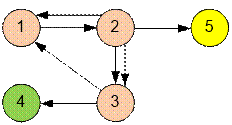
Example

The input graph contains three strongly connected components. From the components consisting of a single vertex (4 and 5), no edges leave. Therefore, it is sufficient to build fire stations exactly in these components.

Algorithm implementation

Store the input graph in the adjacency list g. The reversed graph (the graph in which the directions of all edges are inverted) is stored in the adjacency list gr.

vector<vector<int> > g, gr;

vector<int> used, top, color, repr;

The function dfs1 implements a depth-first search on the input graph. The array top stores the order of vertices corresponding to the moments when their processing is finished during the depth-first traversal.

void dfs1(int v)

{

used[v] = 1;

for (int to : g[v])

if (!used[to]) dfs1(to);

top.push_back(v);

}

The function dfs2 implements a depth-first search on the reversed graph. All vertices visited as a result of recursive calls to dfs2 belong to the same strongly connected component. All such vertices are colored with color c. Vertices that are in the same strongly connected component have the same color.

For each color c, the array repr stores a representative of the corresponding component – any vertex number colored with this color.

void dfs2(int v, int c)

{

color[v] = c;

repr[c] = v;

for (int to : gr[v])

if (color[to] == -1) dfs2(to, c);

}

The main part of the program. Read the input data and build the reversed graph.

scanf("%d %d", &n, &m);

g.resize(n + 1);

gr.resize(n + 1);

for (i = 0; i < m; i++)

{

scanf("%d %d", &a, &b);

g[a].push_back(b);

gr[b].push_back(a);

}

Run a depth-first search on the original graph. The order in which the processing of vertices is completed is stored in the array top.

used.resize(n+1);

for (i = 1; i <= n; i++)

if (!used[i]) dfs1(i);

Run a depth-first search on the reversed graph. The vertices of the reversed graph are processed in the order given by the array top, while the traversal is performed from right to left – from the end of the array to the beginning. For convenience of further processing, the array top is reversed beforehand.

color.assign(n+1, -1);

repr.assign(n+1, -1);

reverse(top.begin(), top.end());

Vertices belonging to the same strongly connected component are colored with the same color. The current color is stored in the variable c.

c = 0;

for (int v : top)

if (color[v] == -1) dfs2(v, c++);

The variable c stores the number of strongly connected components.

used.assign(c, 1);

for (i = 1; i < g.size(); i++)

for (int to : g[i])

Iterate over all edges of the graph (i, to) and check whether the vertices i and to belong to different strongly connected components. This is determined by their different colors. If the vertices are in different components, then there is no need to build a fire station in the component with color color[i], so we set used[color[i]] = 0.

if (color[i] != color[to]) used[color[i]] = 0;

}

Count the number of components c where a fire station should be built.

c = 0;

for (i = 0; i < used.size(); i++)

if (used[i]) c++;

Print the minimum required number of fire stations.

printf("%d\n",c);

For each component with color i from which no edges leave, print its representative (the value repr[i]). These are exactly the house numbers near which fire stations should be built.

for (i = 0; i < used.size(); i++)

if (used[i]) printf("%d ",repr[i]);

printf("\n");