1945

1945. Точки сочленения

Задан неориентированный граф. Найдите все точки сочленения в нем.

Вход. Первая строка содержит два натуральных числа n и m – количество вершин и ребер графа соответственно (n ≤ 2 * 10⁴, m ≤ 2 * 10⁵).

Следующие m строк содержат описание ребер, по одному на строке. Ребро номер i описывается двумя натуральными числами b_i, e_i (1 ≤ b_i, e_i ≤ n) – номерами концов ребра.

Выход. В первой строке выведите количество b точек сочленения в графе. Далее выведите b целых чисел – номера вершин, которые являются точками сочленения, в возрастающем порядке. Каждое число следует выводить в отдельной строке.

Пример входа

Пример выхода

9 12

1 2

2 3

4 5

2 6

2 7

8 9

1 3

1 4

1 5

6 7

3 8

3 9

РЕШЕНИЕ

графы – точки сочленения

Анализ алгоритма

Поиск точек сочленения выполняется при помощи поиска в глубину. Для каждой вершины v вычисляем метки d[v] и up[v]. Вершина v является точкой сочленения, если существует такое ребро (v, to) в дереве обхода в глубину, что выполняется неравенство up[to] ≥ d[v]. Это неравенство означает, что из вершины to, являющейся сыном v, по обратным ребрам из поддерева с вершиной to можно подняться не выше вершины v.

Пример

Граф, приведенный в примере, имеет следующий вид:

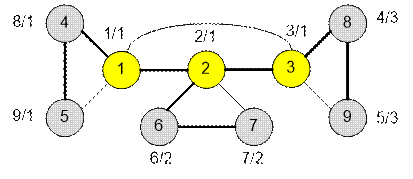
Жирными линиями выделены ребра обхода в глубину. Рядом с каждой вершиной v расположены метки d[v] / up[v]. Точки сочленения выделены цветом.

Вершина 1 точка сочленения, так как для ребра (1, 4): up[4] ≥ d[1] (1 ≥ 1).

Вершина 2 точка сочленения, так как для ребра (2, 6) : up[6] ≥ d[2] (2 ≥ 2).

Вершина 3 точка сочленения, так как для ребра (3, 8) : up[8] ≥ d[3] (3 ≥ 3).

Реализация алгоритма

Граф будем хранить в виде списка смежности g. Массив used используется для отмечания уже пройденных вершин. Для решения задачи будем также использовать два дополнительных массива d и up. Список номеров вершин, которые являются точками сочленения, будем сохранять во множестве ArtPoints.

vector<vector<int> > g;

vector<int> used, d, up;

set<int> ArtPoints;

Функция dfs реализует поиск в глубину из вершины v и совершает поиск точек сочленения. Если v – корень дерева, то устанавливаем p = -1. В переменной children подсчитываем количество детей у вершины – корня. Найденные точки сочленения сохраняются в ArtPoints.

void dfs (int v, int p = -1)

{

int children = 0;

При входе в вершину v отмечаем ее посещенной. Устанавливаем метку d[v] равной текущему значению t. Изначально устанавливаем up[v] равным d[v].

used[v] = 1;

d[v] = up[v] = t++;

Перебираем вершины to, достижимые из v. Расмотрим три случая:

1. (v, to) ребро дерева, которое мы просматриваем в обратном направлении (в этом случае to = p)

2. (v, to) обратное ребро (в этом случае used[to] = 1 и to ≠ p)

3. (v, to) ребро дерева (в этом случае used[to] = 0)

for (int to : g[v])

{

if (to == p) continue;

Если вершина to уже посещена, то (v, to) обратное ребро. Пересчитаем значение up[v].

if (used[to])

up[v] = min (up[v], d[to]);

else

{

Иначе запускаем поиск в глубину из вершины to. Проходим по ребру дерева (v, to). Предком to становится вершина v. Пересчитаем значение up[v].

dfs (to, v);

up[v] = min (up[v], up[to]);

Если up[to] ≥ d[v] и v не корень (p ≠ -1), то вершина v является точкой сочленения.

if ((up[to] >= d[v]) && (p != -1)) ArtPoints.insert(v);

Подсчитаем количество вершин to, в которые поиск в глубину заходит из вершины v.

children++;

}

Если v корень (p = -1) и количество его сыновей в дереве поиска больше 1, то вершина v является точкой сочленения.

if ((p == -1) && (children > 1)) ArtPoints.insert(v);

}

Основная часть программы. Инициализируем массивы. Читаем входные данные.

scanf("%d %d",&n,&m);

g.resize(n+1); used.resize(n+1);

d.resize(n+1); up.resize(n+1);

Считываем неориентированный граф в список смежности g.

for(i = 0; i < m; i++)

{

scanf("%d %d",&a,&b);

g[a].push_back(b);

g[b].push_back(a);

}

Запускаем поиск в глубину. Граф может быть несвязным.

t = 1;

for(i = 1; i <= n; i++)

if (!used[i]) dfs(i);

Выводим количество точек сочленения, а также их самих в возрастающем порядке.

printf("%d\n", ArtPoints.size());

for (int x : ArtPoints)

printf("%d\n", x);

Java реализация

import java.util.*;

public class Main

{

static ArrayList<Integer>[] g;

static int used[], d[], up[];

static int time;

static TreeSet<Integer> ArtPoints = new TreeSet<Integer>();

static void dfs (int v, int p)

{

int i, to, children;

used[v] = 1;

d[v] = up[v] = time++;

children = 0;

for (i = 0; i < g[v].size(); i++)

{

to = g[v].get(i);

if (to == p) continue;

if (used[to] == 1)

up[v] = Math.min(up[v], d[to]);

else

{

dfs (to, v);

up[v] = Math.min(up[v], up[to]);

if ((up[to] >= d[v]) && (p != -1)) ArtPoints.add(v);

children++;

}

if ((p == -1) && (children > 1)) ArtPoints.add(v);

}

@SuppressWarnings("unchecked")

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int m = con.nextInt();

g = new ArrayList[n+1]; // unchecked

used = new int[n+1];

d = new int[n+1];

up = new int[n+1];

for (int i = 0; i <= n; i++)

g[i] = new ArrayList<Integer>();

for (int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g[a].add(b);

g[b].add(a);

}

time = 1;

for(int i = 1; i <= n; i++)

if (used[i] == 0) dfs(i,-1);

System.out.println(ArtPoints.size());

for(int i : ArtPoints)

System.out.println(i);

con.close();

}

Python реализация

Увеличим стек для рекурсии.

import sys

sys.setrecursionlimit(10**6)

g = []

used = []

d = []

up = []

ArtPoints = set()

def dfs(v, p = -1):

global t

children = 0

used[v] = 1

d[v] = up[v] = t

t += 1

Перебираем вершины to, достижимые из v. Расмотрим три случая:

1. (v, to) ребро дерева, которое мы просматриваем в обратном направлении (в этом случае to = p)

2. (v, to) обратное ребро (в этом случае used[to] = 1 и to ≠ p)

3. (v, to) ребро дерева (в этом случае used[to] = 0)

for to in g[v]:

if to == p: continue

Если вершина to уже посещена, то (v, to) обратное ребро. Пересчитаем значение up[v].

if used[to]:

up[v] = min(up[v], d[to])

else:

dfs(to, v)

up[v] = min(up[v], up[to])

Если up[to] ≥ d[v] и v не корень (p ≠ -1), то вершина v является точкой сочленения.

if up[to] >= d[v] and p != -1:

ArtPoints.add(v)

Подсчитаем количество вершин to, в которые поиск в глубину заходит из вершины v.

children += 1

Если v корень (p = -1) и количество его сыновей в дереве поиска больше 1, то вершина v является точкой сочленения.

if p == -1 and children > 1:

ArtPoints.add(v)

Основная часть программы. Инициализируем списки. Читаем входные данные.

n, m = map(int, input().split())

g = [[] for _ in range(n + 1)]

used = [0] * (n + 1)

d = [0] * (n + 1)

up = [0] * (n + 1)

Считываем неориентированный граф в список смежности g.

for _ in range(m):

a, b = map(int, input().split())

g[a].append(b)

g[b].append(a)

Запускаем поиск в глубину. Граф может быть несвязным.

t = 1

for i in range(1, n + 1):

if not used[i]: dfs(i)

Выводим количество точек сочленения, а также их самих в возрастающем порядке.

print(len(ArtPoints))

for x in sorted(ArtPoints):

print(x)