1945. Articulation points
The undirected
graph is given. Find all its articulation points.
Input. The first line contains two positive
integers n and m (n ≤ 2 * 104,
m ≤ 2 * 105) – the number
of vertices and edges respectively.
Each of the next m lines contains the description of an
edge. The edge number i is given
with two positive integers bi, ei (1 ≤ bi, ei ≤ n) – the numbers
of the vertices it connects.
Output. Print in
the first line the number b of
articulation points in a given graph. In the next b lines print the numbers of the
vertices that are articulation points in increasing order.
|
Sample
input |
Sample
output |
9 121 22 34 52 62 78 91 31 41 56 73 8
3 9 |
3 1 2 3 |
SOLUTION
graphs – articulation
points
Algorithm analysis
Search for the
articulation points using the depth first search. For each vertex v, compute the labels d[v] / up[v]. A vertex v is an
articulation point if there exists an edge (v, to) of the depth first search tree such that the inequality up[to]
≥ d[v] holds. This inequality means that from
the vertex to, which is a son of v, along the back
edges from the subtree with the vertex to, one can go no
higher than the vertex v.
Example
Graph gven in a sample, has the form:
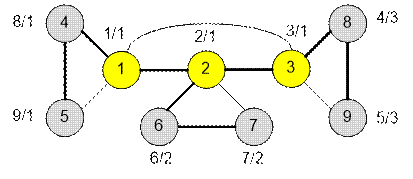
The edges of the depth first search tree are marked with
bold lines. Near each vertex v there are labels d[v] / up[v]. The
articulation points are highlighted in color.
Vertex 1 is an articulation point because for edge (1, 4) up[4]
≥ d[1] (1 ≥ 1).
Vertex 2 is an articulation
point because
for edge (2, 6) up[6] ≥ d[2] (2 ≥ 2).
Vertex 3 is an articulation
point because
for edge (3, 8) up[8] ≥ d[3] (3 ≥ 3).
Algorithm realization
Since the number
of vertices in the graph is large, store the graph in an adjacency list. The array used is used to mark
the already visited vertices. To
solve the problem, we’ll use two additional arrays d and up. The list of
vertices, that are
articulation points, will be saved in the set ArtPoints.
vector<vector<int> > graph;
vector<int> used, d, up;
set<int>
ArtPoints;
The function dfs starts the depth first search from the vertex v and searches for
articulation points. If v is the root of the dfs tree, set p = -1. In the variable children count the
number of children at the root node. Found articulation points are saved in set ArtPoints.
void dfs (int
v, int p = -1)
{
int i, to,
children;
When entering the vertex v, mark it visited. Set the label
d[v] equal to the current timestamp time. Initially set up[v] to be equal to d[v].
used[v] = 1;
d[v] = up[v] = time++;
children = 0;
Iterate over the vertices to that can be reached
from v. It is necessary to consider three cases:
1. (v, to)
is a tree
edge, that
we traverse in the opposite direction (in this case to = p)
2. (v, to)
is a back
edge (in
this case used[to] = 1 and to ≠ p)
3. (v, to)
is a tree
edge (in
this case used[to] = 0)
for (i = 0; i
< graph[v].size(); i++)
{
to = graph[v][i];
if (to ==
p) continue;
If vertex to is visited, then (v, to) is a back edge. Recompute the value of up[v].
if
(used[to])
up[v] = min (up[v], d[to]);
else
{
Otherwise start the depth first search from the vertex to. (v, to) is a tree edge. Recompute up[v].
dfs (to, v);
up[v] = min (up[v], up[to]);
If up[to] ≥ d[v] and v is not a root (p ≠ -1),
then the
vertex v is an articulation point.
if
((up[to] >= d[v]) && (p != -1)) ArtPoints.insert(v);
Count the number of vertices to, into which the
depth first search is run from the vertex v.
children++;
}
}
If v is a root (p = -1) and the number of its sons in dfs
tree is greater than 1, then the vertex v
is an articulation point.
if ((p == -1)
&& (children > 1)) ArtPoints.insert(v);
}
The main part of
the program. Read the
undirected graph into adjacency list graph.
scanf("%d %d",&n,&m);
graph.resize(n+1);
used.resize(n+1);
d.resize(n+1);
up.resize(n+1);
for(i = 0; i < m; i++)
{
scanf("%d
%d",&a,&b);
graph[a].push_back(b); graph[b].push_back(a);
}
Run the depth first search. Graph can be disconnected.
time = 1;
for(i = 1; i <= n; i++)
if (!used[i])
dfs(i);
Print the number of articulation points, as well as them in ascending order.
printf("%d\n",ArtPoints.size());
for(iter = ArtPoints.begin(); iter != ArtPoints.end(); iter++)
printf("%d\n",*iter);
Java realization
import java.util.*;
public class Main
{
static
ArrayList<Integer>[] g;
static int used[], d[], up[];
static int time;
static
TreeSet<Integer> ArtPoints = new
TreeSet<Integer>();
static void dfs
(int v, int p)
{
int i, to, children;
used[v] =
1;
d[v] = up[v] = time++;
children = 0;
for (i = 0;
i < g[v].size();
i++)
{
to = g[v].get(i);
if (to == p) continue;
if (used[to] ==
1)
up[v] =
Math.min(up[v], d[to]);
else
{
dfs
(to, v);
up[v] =
Math.min(up[v], up[to]);
if ((up[to]
>= d[v]) && (p !=
-1)) ArtPoints.add(v);
children++;
}
}
if ((p ==
-1) && (children > 1)) ArtPoints.add(v);
}
@SuppressWarnings("unchecked")
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int m = con.nextInt();
g = new
ArrayList[n+1]; // unchecked
used = new int[n+1];
d = new int[n+1];
up = new int[n+1];
for (int i = 0;
i <= n; i++)
g[i] = new
ArrayList<Integer>();
for (int i = 0;
i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a].add(b);
g[b].add(a);
}
time = 1;
for(int i = 1;
i <= n; i++)
if (used[i] ==
0) dfs(i,-1);
System.out.println(ArtPoints.size());
for(int i : ArtPoints)
System.out.println(i);
con.close();
}
}