1947. Конденсация графа

Найдите количество рёбер в конденсации заданного ориентированного графа.

Конденсацией ориентированного графа G является ориентированный граф G’, вершины которого соответствуют сильно связным компонентам графа G. Ребро в графе G’ проводится тогда и только тогда, когда существует хотя бы одно ребро между вершинами соответствующих компонент связности в графе G’.

В графе-конденсации отсутствуют кратные рёбра.

Вход. Первая строка содержит количество вершин n и количество ребер m (n ≤ 10⁴, m ≤ 10⁵) графа. Каждая из следующих m строк описывает одно ребро графа. i-ое ребро задаётся двумя числами: начальной вершиной b_i и конечной вершиной  e_i (1 ≤ b_i, e_i ≤ n). В графе могут присутствовать кратные ребра и петли.

Выход. Выведите количество ребер в конденсации графа.

Пример входа	Пример выхода
4 4 2 1 3 2 2 3 4 3	2

РЕШЕНИЕ

графы – сильная связность

Анализ алгоритма

Находим компоненты сильной связности графа. Все вершины каждой компоненты сильной связности окрасим в один уникальный цвет. Пусть color[i] – цвет i-ой вершины. Количество использованных цветов равно числу компонент сильной связности.

Перебираем все ребра исходного графа. Если ребро соединяет вершины разных цветов, то оно соответствует ребру в конденсации графа. Для каждого ребра (a, b), такого что color[a] ≠ color[b], добавим во множество s пару (color[a], color[b]). Поскольку используется множество, а не мультимножество, кратные пары учитываться не будут.

Количество элементов во множестве s равно числу рёбер в конденсации графа.

Пример

Граф, приведенный в примере, имеет следующий вид:

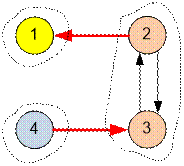
Конденсация графа состоит из трех вершин и двух ребер.

Реализация алгоритма

Входной граф храним в списке смежности g. Обратный граф (граф, в котором направления всех рёбер инвертированы) храним в списке смежности gr. Ребра конденсированного графа будем сохранять во множестве пар s.

vector<vector<int> > g, gr;

vector<int> used, top, color;

set<pair<int,int> > s;

Функция dfs1 реализует поиск в глубину на входном графе. В массив top заносим вершины в порядке завершения их обработки алгоритмом поиска в глубину.

void dfs1(int v)

{

used[v] = 1;

for (int to : g[v])

if (!used[to]) dfs1(to);

top.push_back(v);

}

Функция dfs2 реализует поиск в глубину на обратном графе. Все вершины, посещённые в ходе рекурсивного вызова функции dfs2, принадлежат одной компоненте сильной связности. Все такие вершины окрашиваем в цвет с.

void dfs2(int v, int c)

{

color[v] = c;

for (int to : gr[v])

if (color[to] == -1) dfs2(to, c);

}

Основная часть программы. Читаем входные данные. Строим обратный граф.

scanf("%d %d", &n, &m);

g.resize(n+1);

gr.resize(n+1);

for (i = 0; i < m; i++)

{

scanf("%d %d", &a, &b);

g[a].push_back(b);

gr[b].push_back(a);

}

Запускаем поиск в глубину на входном графе. Порядок завершения обработки вершин сохраняем в массиве top.

used.resize(n+1);

for(i = 1; i <= n; i++)

if (!used[i]) dfs1(i);

Запускаем поиск в глубину на обратном графе. Вершины обратного графа рассматриваем в порядке, обратном массиву top (от последнего элемента к первому). Для удобства дальнейшей обработки перевернём массив top.

color.assign(n + 1, -1);

reverse(top.begin(), top.end());

Вершины, принадлежащие одной компоненте сильной связности, окрашиваем в один и тот же цвет. Текущий цвет хранится в переменной с.

c = 0;

Далее проходим по массиву top слева направо и из каждой ещё не окрашенной вершины запускаем поиск в глубину dfs2.

for (int v : top)

if (color[v] == -1) dfs2(v, c++);

Переменная c содержит количество компонент сильной связности. Перебираем все ребра исходного графа (i, to).

for (i = 1; i < g.size(); i++)

for (int to : g[i])

Проверяем, принадлежат ли вершины i и to разным компонентам сильной связности, то есть окрашены ли они в разные цвета. Если это так, то ребро (i, to) принадлежит конденсации графа, поэтому добавляем во множество s пару (color[i], color[to]). Поскольку используется множество, а не мультимножество, кратные пары учитываться не будут.

if (color[i] != color[to])

s.insert(make_pair(color[i], color[to]));

Выводим количество ребер в конденсации графа.

printf("%d\n",s.size());

Java реализация

import java.util.*;

class Pair implements Comparable<Pair>

{

int x, y;

Pair(int x, int y)

{

this.x = x;

this.y = y;

}

@Override

public int compareTo(Pair a)

{

if (x == a.x) return y - a.y;

return x - a.x;

}

}

public class Main

{

static ArrayList<Integer>[] g, gr;

static int used[], color[];

static Vector<Integer> top = new Vector<Integer>();

static TreeSet<Pair> s = new TreeSet<Pair>();

static void dfs1(int v)

{

used[v] = 1;

for(int i = 0; i < g[v].size(); i++)

{

int to = g[v].get(i);

if (used[to] == 0) dfs1(to);

}

top.add(v);

}

static void dfs2(int v, int c)

{

color[v] = c;

for(int i = 0; i < gr[v].size(); i++)

{

int to = gr[v].get(i);

if (color[to] == -1) dfs2(to,c);

}

}

@SuppressWarnings("unchecked")

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int m = con.nextInt();

g = new ArrayList[n+1];

for(int i = 0; i <= n; i++)

g[i] = new ArrayList<Integer>();

gr = new ArrayList[n+1];

for(int i = 0; i <= n; i++)

gr[i] = new ArrayList<Integer>();

for (int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g[a].add(b);

gr[b].add(a);

}

used = new int[n+1];

for(int i = 1; i <= n; i++)

if (used[i] == 0) dfs1(i);

color = new int[n+1];

Arrays.fill(color, -1);

int c = 0;

for(int i = 1; i <= n; i++)

{

int v = top.get(n-i);

if (color[v] == -1) dfs2(v,c++);

}

for(int i = 1; i < g.length; i++)

for(int j = 0; j < g[i].size(); j++)

{

int to = g[i].get(j);

if (color[i] != color[to])

s.add(new Pair(color[i],color[to]));

}

System.out.println(s.size());

con.close();

}

}