1989. Maximum matching

Graph (V, E) is called bipartite, if its set of vertices V can be divided to two subsets A and B so that any edge from E connects vertex from A with vertex from B.

The matching P is any subset E such that no its two edges have common vertex.

Maximum matching is a matching where the number of edges is maximal.

Find the maximal matching in the bipartite graph.

Input. The first line contains three numbers n, m and k (1 ≤ n, m ≤ 100, 1 ≤ k ≤ 10000), where n is a number of vertices in a set A, m is a number of vertices in a set B, and k is a number of edges in a graph. Each of the next k lines contains two numbers u_i and v_i, meaning that a vertex u_i from set A is connected with an edge with v_i from set B. The vertices in sets A and B are numbered separately, starting from one. All given numbers are integers.

Output. Print in the first line the number of edges l in maximal matching. Then print l rows, two numbers in each. The numbers a_j and b_j in the j-th row mean that matching includes the edge between vertex a_j of the set A and a vertex b_j of the set B. Printed edges must form a maximum matching.

Sample input	Sample output
2 3 4 1 1 1 2 2 2 2 3	2 1 1 2 3

SOLUTION

graphs - maximum matching

Algorithm analysis

This is a classical maximum matching problem, which can either be reduced to flows on a graph, or solved using the augmenting path algorithm.

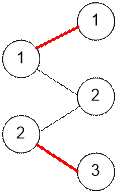
Example

The input graph and maximum matching has the form:

Algorithm realization

Consider the augmenting path algorithm without optimization. The graph is stored in the adjacency list g. To mark the visited vertices during the depth first search, use the array used. To store the current matching, use the array mt.

#define MAX 110

vector<vector<int> > g;

vector<int> used, mt;

The function dfs finds the augmenting path from v with depth first search and returns 1 if such path is found. If an increasing chain is found, the matching is alternated along it.

int dfs(int v)

{

if (used[v]) return 0;

used[v] = 1;

for (int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

if (mt[to] == -1 || dfs(mt[to]))

{

mt[to] = v;

return 1;

}

}

return 0;

}

Finding the maximum matching.

void AugmentingPath(void)

{

Initially the current matching is empty.

mt.assign (m+1, -1);

Start searching for an augmenting path from each vertex of the left part. Set to zero the array of visited vertices used.

for (int i = 1; i <= n; i++)

{

used.assign(n+1, 0);

dfs(i);

}

}

The main part of the program. Read the input data.

scanf("%d %d %d",&n,&m,&k);

g.resize(n+1);

for(i = 0; i < k; i++)

{

scanf("%d %d",&a,&b);

g[a].push_back(b);

}

Find and print the value of the maximum matching.

AugmentingPath();

for (flow = 0, i = 1; i <= m; i++)

if (mt[i] != -1) flow++;

printf("%d\n",flow);

Print the maximum matching itself.

for (i = 1; i <= m; i++)

if (mt[i] != -1) printf("%d %d\n",mt[i],i);

Algorithm realization – optimization

#include <cstdio>

#include <vector>

#include <algorithm>

using namespace std;

vector<vector<int> > g;

vector<int> used, mt, par;

int i, j, ptr;

int n, m, k, a, b, flow;

int dfs(int v)

{

if (used[v]) return 0;

used[v] = 1;

for (int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

if (mt[to] == -1 || dfs(mt[to]))

{

mt[to] = v;

par[v] = to;

return 1;

}

}

return 0;

}

void AugmentingPath(void)

{

int i, run;

mt.assign (m+1, -1);

par.assign (n+1, -1);

for (run = 1; run; )

{

run = 0; used.assign(n+1, 0);

for (i = 1; i <= n; i++)

if ((par[i] == -1) && dfs(i)) run = 1;

}

}

int main(void)

{

scanf("%d %d %d",&n,&m,&k);

g.resize(n+1);

for(i = 0; i < k; i++)

{

scanf("%d %d",&a,&b);

g[a].push_back(b);

}

AugmentingPath();

for (flow = 0, i = 1; i <= m; i++)

if (mt[i] != -1) flow++;

printf("%d\n",flow);

for (i = 1; i <= m; i++)

if (mt[i] != -1) printf("%d %d\n",mt[i],i);

return 0;

}