1990. Доминошки 2

Задана прямоугольная доска, некоторые клетки из которой вырезаны. Определить, можно ли покрыть оставшиеся клетки доминошками.

Вход. В первой строке заданы два целых числа m и n (1 ≤ m, n ≤ 40) – размеры доски. Каждая следующих m строк содержит по n символов. i-ый символ j-ой из этих строк равен "X" (латинское X большое), если клетка вырезана, и "." (точка), если она пуста.

Выход. Выведите в выходной файл "YES", если доску можно покрыть доминошками, и "NO" в противном случае.

Пример входа	Пример выхода
3 2 .X .. X.	YES

РЕШЕНИЕ

графы – максимальный поток

Анализ алгоритма

Построим граф, количество вершин которого равно числу ячеек доски. Перенумеруем ячейки слева направо, сверху вниз. Соединим ребрами все пары соседних пустых ячеек. Далее раскрасим вершины графа в шахматном порядке двумя цветами. Вершины, окрашенные серым, отнесем к первой доле, а белым – ко второй. Таким образом построенный граф оказался двудольным. Найдем величину максимального паросочетания в нем. Оно равно количеству костей домино, которыми можно покрыть пустые клетки доски.

Если удвоенная величина максимального паросочетания равна количеству пустых клеток, то требуемое покрытие существует.

Пример

Построим двудольный граф по заданному примеру.

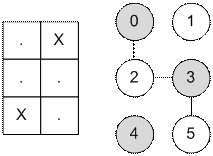
Серые вершины образуют первую долю, белые – вторую. Максимальный поток в соответствующем графе равен 2.

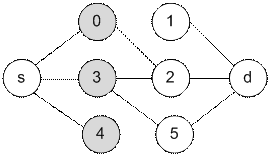
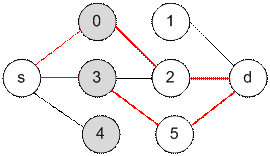
Реализация алгоритма

Доску будем хранить в символьном двумерном массиве s. Граф строим в массиве g.

#define MAX 50

char s[MAX][MAX];

vector<vector<int> > g;

vector<int> mt, used;

Ищем дополняющую цепь из вершины v поиском в глубину.

int dfs(int v)

{

if (used[v]) return 0;

used[v] = 1;

for (int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

if (mt[to] == -1 || dfs(mt[to]))

{

mt[to] = v;

return 1;

}

}

return 0;

}

Основная часть программы. Читаем состояние доски в массив s.

scanf("%d %d\n", &n, &m);

for(i = 0; i < n; i++) gets(s[i]);

Строим граф g. Количество его вершин равно n*m, вершины нумеруются с нуля. Для каждой серой вершины, которой соответствует пустая клетка доски, строим список смежных с ней вершин. Вершину, соответствующую ячейке (i, j), будем считать серой, если сумма i + j четна.

g.resize(n*m); Empty_Cell = 0;

for(i = 0; i < n; i++)

for(j = 0; j < m; j++)

{

if (s[i][j] == 'X') continue;

Empty_Cell++;

if ((i + j) % 2) continue;

Ячейка (i, j) серая и пустая. Она соответствует вершине i*m + j графа. Для каждой соседней с ней пустой ячейки проводим в нее ориентированное ребро. Соседние с (i, j) ячейки перебираем в порядке: левая, правая, верхняя, нижняя.

vector<int> temp;

if (j && (s[i][j-1] == '.')) temp.push_back(i * m + j - 1);

if ((j < m - 1) && (s[i][j+1] == '.')) temp.push_back(i * m + j + 1);

if (i && (s[i-1][j] == '.')) temp.push_back((i - 1) * m + j);

if ((i < n - 1) && (s[i+1][j] == '.')) temp.push_back((i + 1) * m + j);

g[i*m + j] = temp;

}

Ищем дополняющий путь из каждой серой вершины, запуская из нее поиск в глубину.

mt.assign(n*m, -1);

for(i = 0; i < n; i++)

for(j = 0; j < m; j++)

{

if ((i + j) % 2) continue;

used.assign(n*m, 0);

dfs(i * m + j);

}

Вычисляем величину максимального паросочетания в переменной c.

for (c = i = 0; i < n * m; i++)

if (mt[i] != -1) c++;

Если удвоенная величина максимального паросочетания равна количеству пустых клеток, то требуемое покрытие существует.

if (Empty_Cell == 2*c) printf("YES\n");

else printf("NO\n");

Реализация с оптимизацией

#include <cstdio>

#include <algorithm>

#include <vector>

#define MAX 50

using namespace std;

char s[MAX][MAX];

int Empty_Cell, n, m, i, j, c;

vector<vector<int> > g;

vector<int> mt, used, par;

int dfs(int v)

{

if (used[v]) return 0;

used[v] = 1;

for (int i = 0; i < g[v].size(); i++)

{

int to = g[v][i];

if (mt[to] == -1 || dfs(mt[to]))

{

mt[to] = v;

par[v] = 1;

return 1;

}

}

return 0;

}

void AugmentingPath(void)

{

int i, run;

mt.assign(n*m, -1);

par.assign (n*m, -1);

for (run = 1; run; )

{

run = 0; used.assign(n*m, 0);

for(i = 0; i < n; i++)

for(j = 0; j < m; j++)

{

if ((i + j) % 2) continue;

if ((par[i * m + j] == -1) && dfs(i * m + j)) run = 1;

}

}

}

int main(void)

{

scanf("%d %d\n", &n, &m);

for(i = 0; i < n; i++) gets(s[i]);

g.resize(n*m); Empty_Cell = 0;

for(i = 0; i < n; i++)

for(j = 0; j < m; j++)

{

if (s[i][j] == 'X') continue;

Empty_Cell++;

if ((i + j) % 2) continue;

vector<int> temp;

if (j && (s[i][j-1] == '.'))

temp.push_back(i * m + j - 1); // left

if ((j < m - 1) && (s[i][j+1] == '.'))

temp.push_back(i * m + j + 1); // right

if (i && (s[i-1][j] == '.'))

temp.push_back((i - 1) * m + j); // up

if ((i < n - 1) && (s[i+1][j] == '.'))

temp.push_back((i + 1) * m + j); // down

g[i*m + j] = temp;

}

AugmentingPath();

for (c = i = 0; i < n * m; i++)

if (mt[i] != -1) c++;

if (Empty_Cell == 2*c) printf("YES\n");

else printf("NO\n");

return 0;

}