1994. Скобки
Дана последовательность из n круглых скобок и k
запросов на изменение скобки на противоположную (открывающая скобка заменяется
на закрывающую и наоборот). На каждый запрос изменения нужно ответить, стала ли
скобочная последовательность правильной в результате его применения.
Скобочная последовательность называется правильной, если
количество открывающих скобок в ней равно количеству закрывающих, а также в
любом начальном куске последовательности количество открывающих скобок не
меньше количества закрывающих.
Вход. В первой строке содержится n (1 ≤ n ≤
100 000) круглых скобок. Во второй строке содержится количество запросов k (1 ≤ k ≤ 100 000). В каждой из следующих k строк содержится по одному числу p (0 ≤ p < n) – номер скобки, которая меняется на
противоположную.
Выход. Выведите k строк, каждая из которых содержит знак
'+' или '–' в зависимости от того, стала ли после очередного запроса скобочная
последовательность правильной или нет.
|
Пример
входа |
Пример
выхода |
()50011
0 |
- + - + - |
РЕШЕНИЕ
структуры
данных – дерево отрезков, множественная модификация
Анализ алгоритма
Рассмотрим
скобочную структуру. Каждой открывающейся скобке поставим в соответствие число
1, закрывающейся -1. Вычислим частичные суммы полученной последовательности.
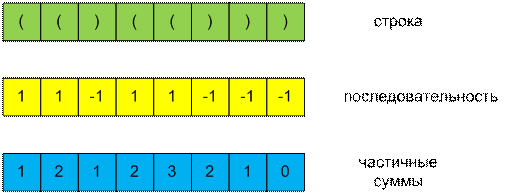
Скобочная
структура будет правильной, если сумма элементов всей последовательности равна
нулю, а все частичные суммы не меньше нуля.
Построим из
частичных сумм скобочной последовательности дерево отрезков. Пусть строка s содержит входную скобочную
последовательность. При поступлении запроса – номера скобки p, которая изменяется, следует:
·
изменить соответствующую скобку в строке s;
·
если ‘(‘ изменяется на ‘)‘, то в соответствующей
последовательности следует 1 заменить на -1, вследствие чего начиная с позиции p значения всех частичных сумм
уменьшится на 2.
·
если ‘) ‘ изменяется на ‘(‘, то в соответствующей
последовательности следует -1 заменить на 1, вследствие чего начиная с позиции p значения всех частичных сумм
увеличится на 2.
После выполнения
каждого запроса за константное время можно определять, является ли текущая
скобочная запись правильной: минимум частичных сумм находится в корне дерева
отрезков, а сумму всех чисел последовательности следует поддерживать в
переменной summa.
Пример
Рассмотрим
строку ”(()(()))”. Построим дерево отрезков из соответствующих ей частичных
сумм {1, 2, 1, 2, 3, 2, 1, 0}. В вершинах указаны значения переменных min. Изначально значения add во всех вершинах равны 0.
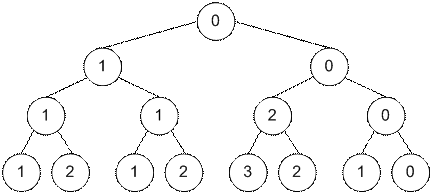
Пусть следует
изменить вторую скобку ‘)’ на ‘(’
(нумерация скобок начинается с нуля). Строка примет вид ”((((()))”. Поскольку в
скобочной последовательности следует -1 заменить на 1, то все частичные суммы
начиная со второй позиции следует увеличиться на 2. Действительно, частичными
суммами строки ”((((()))” будут {1, 2, 3, 4, 5, 4, 3, 2}. В дереве отрезков
следует значение min увеличить на 2
отрезке [2 … 7]. После модификации дерево отрезков примет следующий вид. В
изменившихся вершинах записаны значения min
/ add.
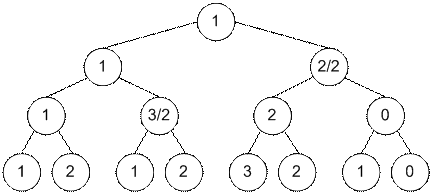
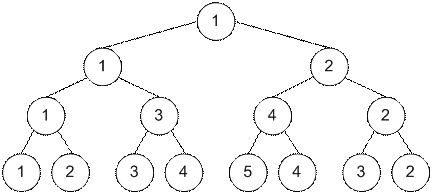
Если, например,
провести проталкивание сразу, то получилось бы дерево отрезков, соответствующее
частичным суммам строки ”((((()))”, то есть последовательности {1, 2, 3, 4, 5,
4, 3, 2}.
Реализация алгоритма
Объявим
структуру дерева отрезков. Она будет поддерживать минимум на отрезке, а также
содержать дополнительную переменную add, используемую для модификации на отрезке. В каждой
вершине дерева переменная min хранит наименьшее значение частичных
сумм на отрезке. В переменной add
содержится значение, которое следует протолкнуть по дереву на один уровень
ниже. То есть прибавить к значению min
левого и правого поддерева, а также добавить его к add левого и правого поддерева тем самым рекурсивно обеспечив
проталкивание значения add до самого
нижнего уровня – то есть до листьев дерева.
struct SegmentTree
{
int add, min,
LeftPos, RightPos;
struct
SegmentTree *Left, *Right;
};
Создадим дерево отрезков из набора
чисел v[L]..v[R].
SegmentTree *build(vector<int> &v, int
L, int R)
{
if (L == R)
{
Строим дерево из одной вершины.
SegmentTree *New = new
SegmentTree ;
New->min = v[L]; New->add = 0;
New->Left = New->Right = NULL;
New->LeftPos = New->RightPos = L;
return New;
}
int m = (L +
R) / 2;
Строим левое и правое поддерево.
SegmentTree *Left = build(v,L,m);
SegmentTree *Right = build(v,m+1,R);
Создаем результирующее дерево Tree с левым поддеревом Left и правым Right.
SegmentTree *Tree = new
SegmentTree;
Tree->Left = Left; Tree->Right = Right;
Пересчитываем значения в корне дерева
через корни поддеревьев. Проталкиваемое значение add устанавливаем равным 0.
Tree->min =
min(Left->min,Right->min);
Tree->LeftPos = Left->LeftPos;
Tree->RightPos = Right->RightPos;
Tree->add = 0;
return Tree;
}
Модификация на отрезке. Прибавим значение
value ко всем ячейкам v[L], …,.v[R].
void AddValue(SegmentTree *&tree, int L, int R, int value)
{
if (L <
tree->LeftPos) L = tree->LeftPos;
if (R >
tree->RightPos) R = tree->RightPos;
if (L > R)
return;
Проведем проталкивание, если add не равно нулю.
if
(tree->add)
{
if
(tree->Left != NULL)
tree->Left->add += tree->add,
tree->Left->min += tree->add;
if
(tree->Right != NULL)
tree->Right->add += tree->add,
tree->Right->min += tree->add;
tree->add = 0;
}
Если корень дерева tree соответствует
отрезку [L..R], то изменяем данные в нем
if
((tree->LeftPos == L) && (tree->RightPos == R))
{
tree->add += value;
tree->min += value;
return;
}
Рекурсивно модифицируем левое и
правое поддерево.
AddValue(tree->Left,L,R,value);
AddValue(tree->Right,L,R,value);
tree->min =
min(tree->Left->min,tree->Right->min);
}
В строке s будем хранить входную скобочную запись, в векторе v частичные
суммы.. Объявим дерево отрезков Tree.
char s[100010];
vector<int> v;
SegmentTree
*Tree;
Основная часть программы. Читаем
скобочную структуру. Вычисляем частичные суммы скобочной последовательности и
заносим ее в вектор v.
gets(s); len =
strlen(s);
for(summa = i = 0; i < len; i++)
{
if (s[i] == '(') summa++; else
summa--;
v.push_back(summa);
}
Строим дерево отрезков.
Tree =
build(v,0,len-1);
Читаем поступающие запросы.
scanf("%d",&k);
while(k--)
{
scanf("%d",&p);
При изменении открывающейся скобки на
закрывающуюся следует вычесть 2 со всех частичных сумм с позиции n до len
– 1.
if
(s[p] == '(')
{
s[p] = ')';
AddValue(Tree,p,n-1,-2);
summa -= 2;
} else
При изменении закрывающейся скобки на
открывающуюся следует добавить 2 ко всем частичным суммам с позиции n до len
– 1.
{
s[p] = '(';
AddValue(Tree,p,n-1,2);
summa += 2;
}
Скобочная запись будет правильной,
если минимум всех частичных сумм не меньше нуля, а сумма всех элементов последовательности
равна нулю.
if
((Tree->min >= 0) && (summa == 0)) printf("+\n");
else printf("-\n");
}
Реализация дерева отрезков при помощи массива
#include <cstdio>
#include <vector>
#include <algorithm>
#include <cstring>
#define MAX 100010
using namespace std;
struct node
{
long long min, add;
} SegTree[4*MAX];
int min(int i, int j)
{
return (i < j) ? i : j;
}
void build (vector<int>
&a, int v, int
LeftPos, int RightPos)
{
if (LeftPos == RightPos)
{
SegTree[v].min =
a[LeftPos];
SegTree[v].add = 0;
}
else
{
int Middle = (LeftPos + RightPos) / 2;
build (a, v*2,
LeftPos, Middle);
build (a, v*2+1,
Middle+1, RightPos);
SegTree[v].min =
min(SegTree[v*2].min,SegTree[v*2+1].min);
SegTree[v].add = 0;
}
}
void Push(int v, int LeftPos, int
Middle, int RightPos)
{
if (SegTree[v].add)
{
SegTree[2*v].add +=
SegTree[v].add;
SegTree[2*v].min +=
SegTree[v].add;
SegTree[2*v+1].add
+= SegTree[v].add;
SegTree[2*v+1].min
+= SegTree[v].add;
SegTree[v].add = 0;
}
}
void AddValue(int v, int LeftPos, int
RightPos,
int L, int
R, int Value)
{
if (L > R) return;
if ((LeftPos == L) && (RightPos == R))
{
SegTree[v].add +=
Value;
SegTree[v].min +=
Value;
return;
}
int Middle = (LeftPos + RightPos) / 2;
Push(v,LeftPos,Middle,RightPos);
AddValue(2*v,
LeftPos, Middle, L, min(Middle,R), Value);
AddValue(2*v+1,
Middle+1, RightPos, max(L,Middle+1), R, Value);
SegTree[v].min =
min(SegTree[2*v].min,SegTree[2*v+1].min);
}
int i, k, n, p, summa;
char s[100010];
vector<int> v;
int main(void)
{
gets(s); n =
strlen(s);
for(summa = i = 0; i < n; i++)
{
// '(' считается равной 1
// ')' считается равной -1
if (s[i] == '(')
summa++; else summa--;
v.push_back(summa);
}
build (v, 1, 0, n -
1);
scanf("%d",&k);
while(k--)
{
scanf("%d",&p);
if (s[p] == '(')
{
s[p] = ')';
AddValue(1,0,n-1,p,n-1,-2);
summa -= 2;
}
else
{
s[p] = '(';
AddValue(1,0,n-1,p,n-1,2);
summa += 2;
}
if ((SegTree[1].min >= 0) && (summa == 0))
printf("+\n");
else printf("-\n");
}
return 0;
}