1994. Brackets
The
sequence of n opening and closing
parentheses are given. You have k
queries for changing a single bracket to opposite (the opening bracket changes
to closing and otherwise). After each query you must answer does the current
sequence of brackets is correct.
The bracket
sequence is called correct if the number of opening brackets equals to the
number of closing, and in any prefix of the sequence the number of opening
brackets is no less then number of closing brackets.
Input. The first line contains n (1 ≤ n ≤ 100 000) parentheses. The second line contains the
number of queries k (1 ≤ k ≤ 100 000). Each of the next k lines contains one number p (0 ≤ p < n) – the bracket number
that must be changed to opposite.
Output. Print k
lines. In each line print either '+' or '–' depending on the correctness of the
current bracket sequence after executing the current query.
Sample
input
()500110 Sample
output
-
+
-
+
-
SOLUTION
data structures – segment tree
Algorithm
analysis
Рассмотрим скобочную структуру. Каждой
открывающейся скобке поставим в соответствие число 1, закрывающейся -1. Вычислим
частичные суммы полученной последовательности. Например, строке”(()(()))”
соответствует последовательность {1, 1, -1, 1, 1, -1, -1, -1}, ее частичные
суммы равны {1, 2, 1, 2, 3, 2, 1, 0}. Скобочная структура будет правильной,
если сумма элементов всей последовательности равна нулю, а все частичные суммы
не меньше нуля.
Построим из частичных сумм скобочной
последовательности дерево отрезков. Пусть строка s содержит входную скобочную последовательность. При поступлении
запроса – номера скобки p, которая
изменяется, следует:
·
изменить
соответствующую скобку в строке s;
·
если ‘(‘
изменяется на ‘)‘, то в соответствующей последовательности следует 1 заменить
на -1, вследствие чего начиная с позиции p
значения всех частичных сумм уменьшится на 2.
·
если
‘) ‘ изменяется на ‘(‘, то в соответствующей последовательности следует -1
заменить на 1, вследствие чего начиная с позиции p значения всех частичных сумм увеличится на 2.
После выполнения каждого запроса за
константное время можно определять, является ли текущая скобочная запись
правильной: минимум частичных сумм находится в корне дерева отрезков, а сумму
всех чисел последовательности следует поддерживать в переменной summa.
Example
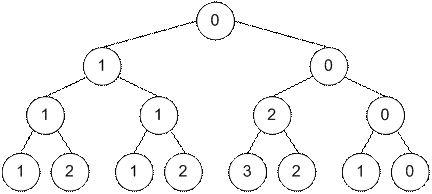
Рассмотрим строку ”(()(()))”. Построим
дерево отрезков из соответствующих ей частичных сумм {1, 2, 1, 2, 3, 2, 1, 0}.
В вершинах указаны значения переменных min.
Изначально значения add во всех
вершинах равны 0.
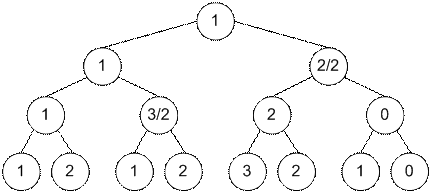
Пусть следует изменить вторую скобку
‘)’ на ‘(’ (нумерация скобок начинается
с нуля). Строка примет вид ”((((()))”. Поскольку в скобочной последовательности
следует -1 заменить на 1, то все частичные суммы начиная со второй позиции
следует увеличиться на 2. Действительно, частичными суммами строки ”((((()))”
будут {1, 2, 3, 4, 5, 4, 3, 2}. В дереве отрезков следует значение min увеличить на 2 отрезке [2 … 7].
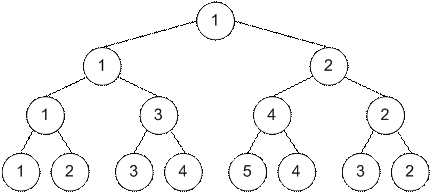
После модификации дерево отрезков примет следующий вид. В изменившихся вершинах
записаны значения min / add.
Если, например, провести проталкивание
сразу, то получилось бы дерево отрезков, соответствующее частичным суммам
строки ”((((()))”, то есть последовательности {1, 2, 3, 4, 5, 4, 3, 2}.
Algorithm
realization
Объявим структуру дерева отрезков. Она
будет поддерживать минимум на отрезке, а также содержать дополнительную
переменную add, используемую для модификации на отрезке.
В каждой вершине дерева переменная min хранит наименьшее
значение частичных сумм на отрезке. В переменной add содержится значение, которое следует протолкнуть по дереву на
один уровень ниже. То есть прибавить к значению min левого и правого поддерева, а также добавить его к add левого и правого поддерева тем самым
рекурсивно обеспечив проталкивание значения add
до самого нижнего уровня – то есть до листьев дерева.
struct SegmentTree
{
int add, min, LeftPos, RightPos;
struct SegmentTree *Left, *Right;
};
Создадим дерево отрезков из набора чисел v[L]..v[R].
SegmentTree *build(vector<int> &v, int
L, int R)
{
if (L == R)
{
Строим дерево из одной вершины.
SegmentTree *New = new SegmentTree ;
New->min = v[L]; New->add = 0;
New->Left = New->Right = NULL;
New->LeftPos = New->RightPos = L;
return New;
}
int m = (L + R) / 2;
Строим левое и правое поддерево.
SegmentTree *Left = build(v,L,m);
SegmentTree *Right = build(v,m+1,R);
Создаем результирующее дерево Tree с левым поддеревом Left
и правым Right.
SegmentTree *Tree = new SegmentTree;
Tree->Left = Left; Tree->Right = Right;
Пересчитываем значения в корне дерева через корни поддеревьев.
Проталкиваемое значение add устанавливаем
равным 0.
Tree->min = min(Left->min,Right->min);
Tree->LeftPos = Left->LeftPos;
Tree->RightPos = Right->RightPos;
Tree->add = 0;
return Tree;
}
Модификация на отрезке. Прибавим значение value ко всем ячейкам v[L], …,.v[R].
void AddValue(SegmentTree *&tree, int
L, int R, int
value)
{
if (L < tree->LeftPos) L =
tree->LeftPos;
if (R > tree->RightPos) R =
tree->RightPos;
if (L > R) return;
Проведем проталкивание, если add не равно нулю.
if (tree->add)
{
if (tree->Left != NULL)
tree->Left->add += tree->add,
tree->Left->min += tree->add;
if (tree->Right != NULL)
tree->Right->add += tree->add,
tree->Right->min += tree->add;
tree->add = 0;
}
Если корень дерева tree соответствует отрезку [L..R], то
изменяем данные в нем
if ((tree->LeftPos == L) &&
(tree->RightPos == R))
{
tree->add += value;
tree->min += value;
return;
}
Рекурсивно модифицируем левое и правое поддерево.
AddValue(tree->Left,L,R,value);
AddValue(tree->Right,L,R,value);
tree->min = min(tree->Left->min,tree->Right->min);
}
В строке s будем
хранить входную скобочную запись, в векторе v частичные суммы.. Объявим дерево
отрезков Tree.
char s[100010];
vector<int>
v;
SegmentTree *Tree;
Основная часть программы. Читаем скобочную структуру.
Вычисляем частичные суммы скобочной последовательности и заносим ее в вектор v.
gets(s); len = strlen(s);
for(summa = i = 0; i < len; i++)
{
if (s[i] == '(')
summa++; else summa--;
v.push_back(summa);
}
Строим дерево отрезков.
Tree = build(v,0,len-1);
Читаем поступающие запросы.
scanf("%d",&k);
while(k--)
{
scanf("%d",&p);
При изменении открывающейся скобки на закрывающуюся следует
вычесть 2 со всех частичных сумм с позиции n
до len – 1.
if (s[p] == '(')
{
s[p] = ')';
AddValue(Tree,p,n-1,-2);
summa -= 2;
} else
При изменении закрывающейся скобки на открывающуюся следует
добавить 2 ко всем частичным суммам с позиции n до len – 1.
{
s[p] = '(';
AddValue(Tree,p,n-1,2);
summa += 2;
}
Скобочная запись будет правильной, если минимум всех частичных
сумм не меньше нуля, а сумма всех элементов последовательности равна нулю.
if ((Tree->min >= 0) &&
(summa == 0)) printf("+\n");
else printf("-\n");
}