2041. День победителей

Приближается Международная олимпиада по информатике и во вьетнамскую команду следует набрать лучших участников со всей страны. К счастью, в команду смогли набрать n хороших участников, пронумерованных от 1 до n. Для выбора среди них наилучших решили организовать три соревнования. Каждый из n конкурсантов принял участие во всех трех соревнованиях, при этом никакие два участника не имеют одинаковых результатов ни в одном из соревнований. Будем говорить что участник А лучше участника В, если А стоит по рангу перед В во всех трех соревнованиях. Участник A является наилучшим, если ни один из других участников не лучше A. Лидеры вьетнамской команды хотят знать число наилучших участников.

Вход. Первая строка содержит количество тестов t (1 ≤ t ≤ 100 ). Далее следует описание t тестов. Первая строка содержит количество участников n (3 ≤ n ≤ 100000). Каждая из следующих n строк задает результаты одного участника и содержит числа a_i, b_i, c_i (1 ≤ a_i, b_i, c_i ≤ n) – ранги i-го участника в первом, втором и третьем соревнованиях.

Выход. Для каждого теста вывести в отдельной строке количество наилучших участников.

Пример входа	Пример выхода
1 3 1 2 3 2 3 1 3 1 2	3

РЕШЕНИЕ

дерево отрезков

Анализ алгоритма

Каждый участник представлен тройкой (a, b, c). Лучше выступет тот участник, у которого ранг лучше (меньше). Например, участник A = (3, 1, 6) лучше участника B = (5, 2, 9) так как его ранги во всех трех соревнованиях лучше. Если A = (3, 1, 6) и B = (5, 2, 3), то участники А и B не сравнимы между собой, они оба относительно друг друга являются наилучшими (никакой другой участник не является лучше А или лучше B). Отсортируем тройки по первой компоненте (по условию все значения a_i, b_i, c_i между собой различны).

Рассмотрим на плоскости n точек с координатами (b_i, c_i). Если относительно точки (b_i, c_i) не существует такой точки (b_j, c_j), что j < i и которая находится одновременно левее и ниже, то она является превосходной.

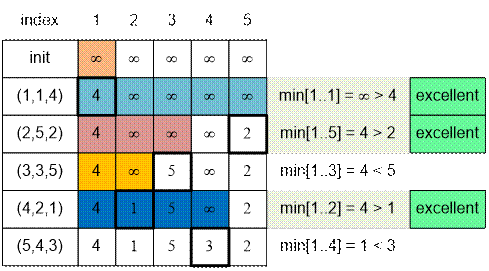
Рассмотрим массив a[1; n], каждый элемент которого изначально равен бесконечности. Построим по нему дерево отрезков, поддерживающего операцию минимума. Рассмотрим пары (b_i, c_i) в порядке возрастания их соответствующих a_i. Найдем минимум на отрезке [1; b_i]. Если он больше c_i, то в квадранте левее и ниже от (b_i, c_i) не лежит ни одна из уже рассмотренных точек. Следовательно текущая тройка превосходная. Далее установим a[b_i] = c_i и перейдем к рассмотрению следующей точки.

Пример

Рассмотрим следующий тест:

1

5

1 1 4

2 5 2

3 3 5

4 2 1

5 4 3

Тройки для удобства уже отсортированы по первой компоненте. Разместим на плоскости пары (b_i, c_i):

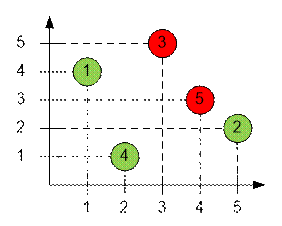
Зеленым цветом отмечены превосходные тройки.

Реализация алгоритма

Объявим константы и рабочие структуры данных. Дерево отрезков SegmentTree будет поддерживать минимум.

#define MAX 100010

#define INF 2000000000

struct Strength

{

int a, b, c;

} Fight[MAX];

int SegmentTree[4*MAX];

Участников будем упорядочивать по возрастанию первой компоненты.

int cmp(Strength x, Strength y)

{

return x.a < y.a;

}

Построение дерева отрезков. Во все его вершины заносим значение +∞.

void BuildTree(int Vertex, int LeftPos, int RightPos)

{

if (LeftPos == RightPos) SegmentTree[Vertex] = INF;

else

{

int Middle = (LeftPos + RightPos) / 2;

BuildTree(2*Vertex, LeftPos, Middle);

BuildTree(2*Vertex+1, Middle+1, RightPos);

}

SegmentTree[Vertex] = INF;

}

Вычисление минимума на отрезке.

int GetMin(int Vertex, int LeftPos, int RightPos, int Left, int Right)

{

if (Left > Right) return INF;

if ((Left == LeftPos) && (Right == RightPos))

return SegmentTree[Vertex];

int Middle = (LeftPos + RightPos) / 2;

return min(GetMin(2*Vertex, LeftPos, Middle, Left,

min(Right,Middle)),

GetMin(2*Vertex+1, Middle+1, RightPos,

max(Left,Middle+1),Right));

}

Единичное присваивание: m[Position] = NewValue.

void update(int Vertex, int LeftPos, int RightPos, int Position,

int NewValue)

{

if (LeftPos == RightPos) SegmentTree[Vertex] = NewValue;

else

{

int Middle = (LeftPos + RightPos) / 2;

if (Position <= Middle)

update(2*Vertex, LeftPos, Middle, Position, NewValue);

else update(2*Vertex+1, Middle+1, RightPos, Position, NewValue);

SegmentTree[Vertex] =

min(SegmentTree[2*Vertex],SegmentTree[2*Vertex+1]);

}

}

Основная часть программы. Читаем входные данные.

scanf("%d",&tests);

while(tests--)

{

scanf("%d",&n);

for(i = 0; i < n; i++)

scanf("%d %d %d",&Fight[i].a, &Fight[i].b, &Fight[i].c);

Сортируем участников по первой компоненте. У кого меньшее место – тот и победитель.

sort(Fight,Fight+n,cmp);

Строим дерево отрезков.

BuildTree(1,1,n);

Последовательно обрабатываем участников. В переменной Result подсчитываем количество наилучших участников.

for(Result = i = 0; i < n; i++)

{

int c = GetMin(1,1,n,1,Fight[i].b);

if (c > Fight[i].c)

{

Result++;

update(1,1,n,Fight[i].b,Fight[i].c);

}

}

Выводим ответ.

printf("%d\n",Result);

}