2103. Knapsack

Vasya is going to hike with fellow programmers and decided to take a responsible approach to the choice of what he will take with him. Vasya has n things that he could take with him in his knapsack. Every thing weighs 1 kilogram. Things have different “usefulness” for Vasya.

The hiking is going to be very long, so Vasya would like to carry a knapsack of weight no more than w kilo.

Help him to determine the total “usefulness” of things in his knapsack if the weight of backpack can be no more than w kilo.

Input. The first line contains integers w and n (1 ≤ w, n ≤ 20). The second line contains n integers c_i (1 ≤ c_i ≤ 1000) – the “usefulness” for each thing.

Output. Print the total “usefulness” of things that Vasya can take with him.

Sample imput	Sample output
2 3 1 5 3	8

SOLUTION

greedy

Algorithm analysis

Let's use the greedy approach. Sort things in order of non-increasing usefulness. Since the weight of each item is 1 kilogram, Vasya should take min(w, n) of the most useful items.

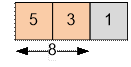
Example

Consider the sample from the problem statement. Sort three given items in descending order. And take the two with the greatest usefulness.

Algorithm realization

Read the input data. Store the usefulness of things in the array cost.

scanf("%d %d", &w, &n);

cost.resize(n);

for(i = 0; i < n; i++)

scanf("%d",&cost[i]);

Sort the usefulness of things in non-decreasing order.

sort(cost.begin(),cost.end(),greater<int>());

Sum up the usefulness of things.

s = 0;

for(i = 0; i < min(w,n); i++)

s += cost[i];

Print the answer.

printf("%d\n",s);

Java realization

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int w = con.nextInt();

int n = con.nextInt();

Integer cost[] = new Integer[n];

for(int i = 0; i < n; i++)

cost[i] = con.nextInt();

Arrays.sort(cost,Collections.reverseOrder());

int s = 0;

for(int i = 0; i < Math.min(w,n); i++)

s += cost[i];

System.out.println(s);

con.close();

}

}