2157. Сумма

Родители подарили Роману неориентированный связный взвешенный граф с n вершинами и n – 1 ребрами. Роман хочет найти суммарную длину всех путей между парами вершин в графе. Длиной пути считается сумма весов всех рёбер, входящих в него. Поскольку путь из вершины u в вершину v совпадает с путём из v в u, Роман считает их одним и тем же и не различает.

Вход. Первая строка содержит количество вершин в графе n (2 ≤ n ≤ 10⁵). Следующие n – 1 строк описывают ребра. Каждая строка содержит три целых числа: номера вершин, соединенных ребром (вершины пронумерованы числами от 1 до n), и вес ребра.

Выход. Выведите сумму длин всех различных путей между парами вершин, вычисленную по модулю 10⁹.

Пример входа 1	Пример выхода 1
3 1 2 1 1 3 3	8
Пример входа 2	Пример выхода 2
6 1 2 5 1 3 1 2 4 2 2 5 4 2 6 3	90

В первом примере все пути в дереве следующие: 1 – 2, 1 – 3, 2 – 1 – 3. Их длины равны соответственно 1, 3 и 4, а сумма этих длин равна 1 + 3 + 4 = 8.

РЕШЕНИЕ

графы – поиск в глубину - дерево

Анализ алгоритма

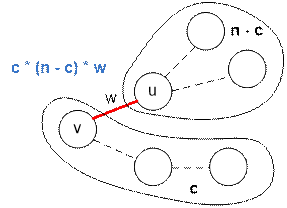
Запустим поиск в глубину из произвольной вершины дерева. Рассмотрим ребро (u, v) с весом w. Пусть количество вершин в поддереве с корнем v равно с. Тогда с одной стороны ребра находится c вершин, а с другой n – c вершин. Ребро (u, v) входит в c * (n – c) различных путей между парами вершин. Следовательно, вклад ребра (u, v) в суммарную длину всех путей равен c * (n – c) * w. Остается перебрать все ребра с помощью поиска в глубину и просуммировать их вклад в общую сумму длин путей.

Пример

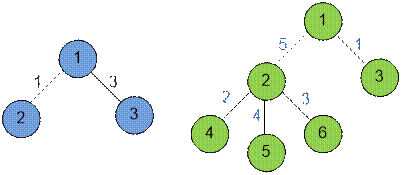
Графы, приведенные в примерах, имеют вид:

Рассмотрим вклад ребер в общую сумму длин всех путей в первом примере.

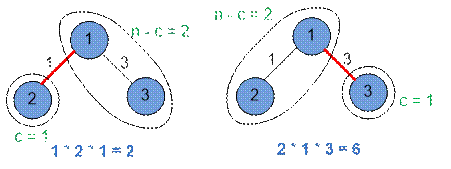
Ребро (1, 2) весом 1 принадлежит двум путям:

· 1 – 2;

· 2 – 1 – 3;

Его вклад в общую сумму равен 1 * 2 * 1 = 2.

Ребро (1, 3) весом 3 принадлежит двум путям:

· 1 – 3;

· 2 – 1 – 3;

Его вклад в общую сумму равен 2 * 1 * 3 = 6.

Суммарная длина всех путей равна 2 + 6 = 8.

Во втором примере рассмотрим вклад ребра (1, 2) весом 5 в общую сумму длин всех путей.

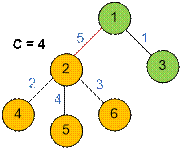
Количество вершин в поддереве с корнем в вершине 2 равно с = 4 (включая саму вершину 2). Тогда с другой стороны ребра (1, 2) находится n – c = 6 – 4 = 2 вершины. Следовательно, количество различных путей, проходящих через ребро (1, 2), равно c * (n – c) = 4 * 2 = 8.

Действительно, такими путями являются все пары вершин, в которых одна вершина лежит в поддереве вершины 2, а другая – вне его:

1 – 2, 1 – 2 – 4, 1 – 2 – 5, 1 – 2 – 6,

3 – 1 – 2, 3 – 1 – 2 – 4, 3 – 1 – 2 – 5, 3 – 1 – 2 – 6

Вклад ребра (1, 2) весом 5 в сумму длин всех путей составляет

c * (n – c) * w = 4 * 2 * 5 = 40

Реализация алгоритма

Объявим значение модуля MOD.

#define MOD 1000000000

Входной взвешенный граф храним в списке смежности g.

vector<vector<pair<int,int> > > g;

Функция dfs реализует поиск в глубину из вершины v возвращает количество вершин в поддереве с корнем v (включая саму вершину v). Подсчет этих вершин ведётся в переменной cnt. Изначально полагаем cnt = 1, поскольку само поддерево уже содержит вершину v.

int dfs(int v, int p = -1)

{

int cnt = 1;

for (auto edge : g[v])

{

int to = edge.first;

int w = edge.second;

Рассмотрим ребро (v, to) с весом w. Вычисляем количество вершин c в поддереве с корнем в вершине to. Тогда с одной стороны ребра находятся c вершин, а с другой n – c вершин. Ребро (v, to) входит в c * (n – c) различных путей между парами вершин.

Таким образом, вклад ребра (v, to) в суммарную длину всех путей равен

c * (n – c) * w

if (to != p)

{

int c = dfs(to, v);

res = (res + 1LL * c * (n - c) * w) % MOD;

cnt += c;

}

}

return cnt;

}

Основная часть программы. Читаем входной взвешенный граф в список смежности g.

scanf("%d", &n);

g.resize(n + 1);

for (i = 1; i < n; i++)

{

scanf("%d %d %d", &u, &v, &d);

g[u].push_back({v, d});

g[v].push_back({u, d});

}

Запускаем поиск в глубину из вершины 1. Вершины графа нумеруются от 1 до n.

dfs(1);

Выводим ответ.

printf("%lld\n",res);

Java реализация

import java.util.*;

import java.io.*;

class Edge

{

int to;

int weight;

public Edge(int to, int weight)

{

this.to = to;

this.weight = weight;

}

}

public class Main

{

static int MOD = 1000000000;

static ArrayList<Edge>[] g;

static int n, m;

static long res;

static int dfs(int v, int p)

{

int cnt = 1;

for(Edge edge : g[v])

{

int to = edge.to;

int w = edge.weight;

if (to != p)

{

int c = dfs(to, v);

res = (res + 1L * c * (n - c) * w) % MOD;

cnt += c;

}

}

return cnt;

}

public static void main(String[] args)

{

FastScanner con = new FastScanner(System.in);

n = con.nextInt();

g = new ArrayList[n+1]; // unchecked

for (int i = 0; i <= n; i++)

g[i] = new ArrayList<Edge>();

for (int i = 1; i < n; i++)

{

int u = con.nextInt();

int v = con.nextInt();

int d = con.nextInt();

g[u].add(new Edge(v,d));

g[v].add(new Edge(u,d));

}

dfs(1,-1);

System.out.println(res);

}

}

class FastScanner

{

BufferedReader br;

StringTokenizer st;

public FastScanner(InputStream inputStream)

{

br = new BufferedReader(new InputStreamReader(inputStream));

st = new StringTokenizer("");

}

public String next()

{

while (!st.hasMoreTokens())

{

try

{

st = new StringTokenizer(br.readLine());

} catch (Exception e)

{

return null;

}

}

return st.nextToken();

}

public int nextInt()

{

return Integer.parseInt(next());

}

}

Python реализация

Объявим значение модуля MOD.

MOD = 1000000000

Функция dfs реализует поиск в глубину из вершины v возвращает количество вершин в поддереве с корнем v (включая саму вершину v). Подсчет этих вершин ведётся в переменной cnt. Изначально полагаем cnt = 1, поскольку само поддерево уже содержит вершину v.

def dfs(v, p = -1):

global res

cnt = 1

for to, w in g[v]:

Рассмотрим ребро (v, to) с весом w. Вычисляем количество вершин c в поддереве с корнем в вершине to. Тогда с одной стороны ребра находятся c вершин, а с другой n – c вершин. Ребро (v, to) входит в c * (n – c) различных путей между парами вершин.

Таким образом, вклад ребра (v, to) в суммарную длину всех путей равен

c * (n – c) * w

if to != p:

c = dfs(to, v)

res = (res + c * (n - c) * w) % MOD

cnt += c

return cnt

Основная часть программы. Читаем входные данные.

n = int(input())

g = [[] for _ in range(n + 1)]

res = 0

for _ in range(n - 1):

u, v, d = map(int, input().split())

g[u].append((v, d))

g[v].append((u, d))

Запускаем поиск в глубину из вершины 1. Вершины графа нумеруются от 1 до n.

dfs(1)

Выводим ответ.

print(res)