2261. Защита королевства

Теодор реализует новую стратегию игры "Оборона Царства". На каждом уровне игрок защищает королевство, которое представлено прямоугольной сеткой ячеек. В некоторых клетках игрок строит арбалетные башни. Башня защищает все клетки в той же строке и том же столбце. Никакие две башни не находятся на одной строке или столбце.

Штрафом положения является количество клеток в крупнейшем незащищенном прямоугольнике. Например, положение, показанное на рисунке имеет штраф 12.

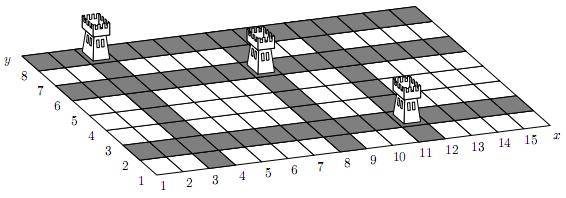
Помогите Теодору написать программу, вычисляющую штраф в заданной позиции.

Вход. Первая строка содержит три целых числа: w – ширина сетки, h – высота сетки и n – количество арбалетных башен (1 ≤ w, h ≤ 40000; 0 ≤ n ≤ min(w, h)).

Каждая из следующих n строк содержит два целых числа x_i и y_i – координаты клетки с башней (1 ≤ x_i ≤ w; 1 ≤ y_i ≤ h).

Выход. Вывести одно число – количество клеток в наибольшем прямоугольнике, не защищенном башнями.

Пример входа	Пример выхода
15 8 3 3 8 11 2 8 6	12

РЕШЕНИЕ

жадные алгоритмы

Анализ алгоритма

Добавим две граничные башни с координатами (0, 0) и (w + 1, h + 1). Отсортируем абсциссы x_i башен и их ординаты y_i. Найдем максимальное расстояние между соседними парами абсцисс dx и ординат dy. Произведение dx * dy равно количеству клеток в крупнейшем незащищенном прямоугольнике.

Реализация алгоритма

Объявим массивы x и y в которых будем хранить координаты башен.

#define MAX 40010

int x[MAX], y[MAX];

Читаем входные данные.

scanf("%d %d %d",&w,&h,&n);

for(i = 0; i < n; i++)

scanf("%d %d",&x[i],&y[i]);

Добавим две башни с координатами (0, 0) и (w + 1, h + 1), увеличим количество башен n на 2.

x[n] = y[n] = 0;

x[n+1] = w + 1; y[n+1] = h + 1;

n += 2;

Сортируем массив абсцисс и ординат.

sort(x,x+n);

sort(y,y+n);

Ищем максимальное расстояние dx между соседними абсциссами.

dx = 0;

for(i = 0; i < n - 1; i++)

if (x[i+1] - x[i] > dx) dx = x[i+1] - x[i];

Ищем максимальное расстояние dy между соседними ординатами.

dy = 0;

for(i = 0; i < n - 1; i++)

if (y[i+1] - y[i] > dy) dy = y[i+1] - y[i];

Выводим размер максимального незащищенного прямоугольника.

printf("%lld\n",1LL * (dx - 1) * (dy - 1));