2267. Путешествие

Армия Речи Посполитой движется из города Костромы в деревню Домнино. Во главе армии стоят два гетмана – Стефан и Константин.

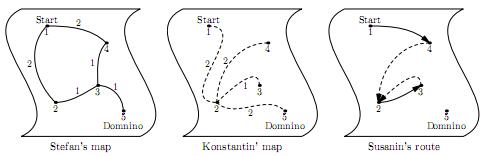
Стефан приобрел карту Костромской области, и каждую ночь он ведет армию от одной деревни к другой по одной из указанных дорог. Константин же раздобыл карту секретных троп, и каждый день он ведет армию по одной из этих троп. Перед каждым переходом каждый из гетманов спрашивает у проводника Ивана Сусанина, какой маршрут лучше выбрать.

На карте у Стефана указана длина каждой дороги, поэтому он знает минимальные расстояния между любой деревней и деревней Домнино по своей карте. Аналогично, Константин знает кратчайшие расстояния до Домнино, если следовать по тропам согласно его карте.

Иван Сусанин, будучи тайным агентом, не хочет разоблачить себя. Поэтому каждый раз он выбирает дорогу (для Стефана) и тропу (для Константина) так, чтобы кратчайшее расстояние до деревни Домнино, согласно карте того гетмана, который задает вопрос, строго уменьшалось.

Помогите Ивану найти самый длинный возможный путь до деревни Домнино.

Вход. Первая строка содержит три целых числа n, s и t (2 ≤ n ≤ 1000, 1 ≤ s, t ≤ n) – количество деревень в Костромской области, а также номера начальной деревни и деревни Домнино. Деревни пронумерованы числами от 1 до n. Начальная деревня и деревня Домнино различны.

Далее следуют два блока, каждый из которых задает карту: первый блок – карту Стефана, второй — карту Константина.

Первая строка каждого блока содержит целое число m (n – 1 ≤ m ≤ 10⁵) – количество дорог/троп между деревнями. Каждая из следующих m строк содержит три целых числа a, b и l, описывающих дорогу или тропу между деревнями a и b длиной l (1 ≤ a, b ≤ n, 1 ≤ l ≤ 10⁶).

Армия может двигаться в любом направлении по дорогам и тропам. Известно, что по карте каждого гетмана можно добраться из любой деревни в любую. Армия стартует вечером из начальной деревни, продвигаясь по одной дороге каждую ночь и по одной тропе каждый день.

Выход. Выведите длину самого длинного пути, по которому Иван Сусанин может водить армию Речи Посполитой, пока она не достигнет деревни Домнино (с учетом дорог и троп). Если Иван может водить армию бесконечно, не достигая Домнино, выведите “-1”.

Пример входа 1	Пример выхода 1
5 1 5 5 1 2 2 1 4 2 2 3 1 3 4 1 5 3 1 4 1 2 2 2 4 2 2 3 1 2 5 2	-1
Пример входа 2	Пример выхода 2
3 1 3 4 1 2 10 2 3 10 1 3 20 2 3 30 4 2 1 10 1 3 10 1 1 10 2 3 10	20

РЕШЕНИЕ

графы – алгоритм Дейкстры

Анализ алгоритма

Построим два графа: граф дорог g[0] и граф троп g[1]. Далее вычислим кратчайшие расстояния от деревни Домнино t до всех деревень:

· По карте Стефана: d[0][i] – минимальное расстояние от t до деревни i;

· По карте Константина: d[1][i] – минимальное расстояние от t до деревни i;

Затем рассмотрим граф, вершинами которого являются пары (v, parity):

· v – номер деревни;

· parity = 0 (ночь, передвижение по дорогам), parity = 1 (день, передвижение по тропам).

Армия начинает путь вечером из начальной деревни, двигаясь ночью по дороге (parity = 0). Запускаем поиск в глубину из вершины (s, 0) по следующим правилам:

· из (v, 0) (ночь) идём по дороге в (u, 1), если d[0][u] < d[0][v];

· из (v, 1) (день) идём по тропе в (u, 0), если d[1][u] < d[1][v].

Находясь в состоянии (v, parity), перебираем только допустимые переходы, то есть такие, при которых расстояние до Домнино строго уменьшается. Среди них ищем путь максимальной длины.

Напомним, что каждый из гетманов стремится двигаться так, чтобы расстояние по его карте уменьшалось (при этом он не обязан следовать кратчайшему пути).

При выполнении поиска в глубину будем поддерживать следующую динамику:

· dp[type][v] – максимальная длина пути от v до t, начиная с типа type.

Для каждого допустимого перехода:

· Рекурсивно вызываем dfs(to, type ^ 1) – переход в противоположную фазу.

· Обновляем значение dp[type][v]:

dp[type][v] = max(dp[type][v], dp[type ^ 1][to] + weight);

Таким образом, мы выбираем наилучший следующий ход, который приводит к максимальной суммарной длине пути. Это аналог стандартного поиска самого длинного пути в DAG (ориентированном ациклическом графе), где направление рёбер определяется уменьшением кратчайшего расстояния.

Движение разрешено только по рёбрам, ведущим к вершинам с меньшим расстоянием до Домнино. Однако в задаче присутствуют два графа – два типа рёбер: дороги и тропы, – а переходы между ними чередуются: ночь (дорога), день (тропа), ночь, день и так далее. Именно из-за этого чередования карт (дорог и троп) может возникнуть цикл между вершинами, даже несмотря на то, что в каждом отдельном графе (по одной карте) движение всегда идёт по убывающему расстоянию.

Если при поиске в глубину мы вновь попадаем в вершину, которая уже находится в стеке обработки, это означает, что обнаружен цикл.

Реализация алгоритма

Объявим константы.

#define INF 2e18

#define MAXN 1005

Объявим используемые структуры данных:

· g[0] и g[1] – списки смежности для графов дорог и троп соответственно.

· d[0] и d[1] – кратчайшие расстояния от деревни Домнино t до всех остальных деревень.

· dp[0] и dp[1] – максимальная длина пути от вершины v до t, если стартовать из v по дороге (type = 0) или по тропе (type = 1).

· used[0] и used[1] – метки вершин при обходе в глубину для графов дорог и троп соответственно.

vector<pair<int, int>> g[2][MAXN];

long long d[2][MAXN];

long long dp[2][MAXN];

int used[2][MAXN];

Функция dijkstra вычисляет кратчайшие расстояния от деревни Домнино t до всех остальных деревень либо по дорогам (type = 0), либо по тропам (type = 1).

void dijkstra(int type)

{

for (int i = 1; i <= n; i++)

d[type][i] = INF;

d[type][t] = 0;

priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<pair<long long, int>>> pq;

pq.push({ 0, t });

while (!pq.empty())

{

pair<long long, int> top = pq.top();

pq.pop();

long long dist = top.first;

int v = top.second;

if (dist > d[type][v]) continue;

for (auto edge : g[type][v])

{

int to = edge.first;

int w = edge.second;

if (d[type][to] > d[type][v] + w)

{

d[type][to] = d[type][v] + w;

pq.push({ d[type][to], to });

}

}

}

}

Функция dfs выполняет поиск в глубину и находит самый длинный путь при движении по чередующимся картам, начиная из деревни v по дороге (type = 0) или по тропе (type = 0). Если при таком чередующемся движении возникает возможность попасть в цикл, функция возвращает -1.

void dfs(int v, int type)

{

Вершина v в графе g[type] становится серой.

used[type][v] = 1;

Инициализируем динамику.

dp[type][v] = 0;

Перебираем ребра, исходящие из вершины v в графе g[type].

for (auto edge : g[type][v])

{

int to = edge.first;

int weight = edge.second;

Переход из вершины v в вершину to возможен только в том случае, если расстояние от to до Домнино меньше, чем расстояние от v до Домнино.

if (d[type][to] < d[type][v])

{

Если вершина to в графе g[type ^ 1] уже находится в процессе обхода (помечена как “серая”), значит, обнаружен цикл – возвращаем -1.

if (used[type ^ 1][to] == 1)

{

cout << -1 << endl;

exit(0);

}

Если вершина to в графе g[type ^ 1] еще не посещена, продолжаем из нее поиск в глубину.

if (used[type ^ 1][to] == 0)

dfs(to, type ^ 1);

После обработки всех допустимых переходов пересчитываем динамику, выбирая максимальную длину пути от вершины v в графе g[type] до Домнино.

dp[type][v] = max(dp[type][v], dp[type ^ 1][to] + weight);

}

}

Вершина v в графе g[type] помечается черной.

used[type][v] = 2;

}

Основная часть программы. Читаем входные данные. Строим графы дорог и троп.

scanf("%d %d %d", &n, &s, &t);

scanf("%d", &m1);

for (i = 0; i < m1; i++)

{

scanf("%d %d %d", &a, &b, &len);

g[0][a].push_back({ b, len });

g[0][b].push_back({ a, len });

}

scanf("%d", &m2);

for (i = 0; i < m2; i++)

{

scanf("%d %d %d", &a, &b, &len);

g[1][a].push_back({ b, len });

g[1][b].push_back({ a, len });

}

Вычисляем кратчайшие расстояния от деревни Домнино t до всех остальных деревень – отдельно для карты дорог и для карты троп.

dijkstra(0);

dijkstra(1);

При помощи поиска в глубину находим самый длинный путь при движении по чередующимся картам, начиная из деревни s по дороге.

dfs(s, 0);

Выводим ответ. Стартовая точка – деревня s, движение начинается по дороге.

printf("%lld\n", dp[0][s]);