2267. Journey
The army
of the Polish–Lithuanian Commonwealth is marching from the city of Kostroma to
the village of Domnino. The army is led by two hetmans – Stefan and Konstantin.
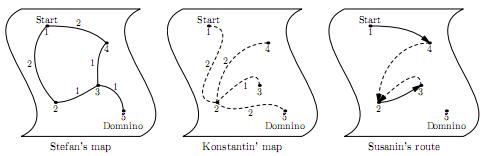
Stefan
has a map of the Kostroma region, which shows all the roads between villages.
Each night, he leads the army from one village to another using one of these
roads. Konstantin, on the other hand, has obtained a map of secret trails, and
during the day, he leads the army along one of these paths. Before each
movement, each hetman consults the guide, Ivan Susanin, to determine the best
route.
Stefan’s map shows the length of each road, so he
can calculate the shortest distance from any village to Domnino using his map.
Similarly, Konstantin knows the shortest distances according to his map of
trails.
Ivan
Susanin, being a secret agent, wants to avoid raising suspicion. Therefore,
each time he selects a road (for Stefan) and a trail (for Konstantin) such that
the shortest distance to the village of Domnino, according to the respective
hetman’s map, strictly decreases.
Help Ivan
determine the maximum possible length of the route to the village of Domnino.
Input. The first line
contains three integers n, s and t (2 ≤ n ≤ 1000, 1 ≤ s, t
≤ n) – the number of villages in the Kostroma region, the starting
village number, and the village number of Domnino, respectively. Villages are
numbered from 1 to n. It is guaranteed that s ≠ t.
Then follow two
blocks, each describing a map: the first block is Stefan’s map, the second one
is Konstantin’s.
The first line
of each block contains an integer m (n – 1 ≤ m ≤ 105) –
the number of roads or trails. Each of the following m lines contains three integers a, b and l (1 ≤ a, b ≤ n, 1 ≤
l ≤ 106) describing a connection between
villages a and b of length l.
Movement along
roads and trails is allowed in both directions. It is guaranteed that each map
allows travel between any pair of villages. The army begins its journey in the
evening from village s, traveling one road per night and one trail
per day.
Output. Print a single
integer – the maximum
possible length of the route to village Domnino (considering alternating road
and trail movement). If Ivan Susanin can lead the army indefinitely without
reaching Domnino, print “-1”.
|
Sample
input 1 |
Sample
output 1 |
5 1 551 2 21 4 22 3 13 4 15 3 141 2 22 4 22 3 12 5 2 |
-1 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
3 1 341 2 102 3 101 3 202 3 3042 1 101 3 101 1 102 3 10 |
20 |
SOLUTION
graphs – Dijkstra
Algorithm
analysis
Ñonstruct two graphs: the
road graph g[0] and the trail graph g[1]. Next, compute the shortest
distances from the village Domnino t to all villages:
·
According to Stefan’s map: d[0][i] – the minimum distance
from t to
village i;
·
According to Konstantin’s map: d[1][i] – the minimum distance
from t to
village i;
Then consider a graph
whose vertices are pairs (v, parity):
·
v – the village number;
·
parity = 0 (night, movement along roads), parity = 1 (day, movement along trails).
The army starts its
journey in the evening from the initial village, moving at night along a road (parity =
0). Run a
depth-first search from the vertex (s, 0) following these rules:
·
from (v, 0) (night) go along a road to (u, 1) if d[0][u] <
d[0][v];
·
from (v, 1) (day) go along a trail to (u, 0) if d[1][u] <
d[1][v].
Being in the
state (v, parity), consider only allowed transitions – that is,
those for which the distance to Domnino strictly decreases. Among these, look
for the path of maximum length.
Recall that each
of the hetmans tries to move so that the distance according to their own map
decreases (however, they are not required to follow the shortest path).
During the
depth-first search, maintain the following dynamic programming state:
·
dp[type][v] – the maximum length of a path from v
to t, starting from phase type.
For each allowed
transition:
·
Recursively call dfs(to, type
^ 1) – transition
to the opposite phase.
·
Update the value of dp[type][v]:
dp[type][v] = max(dp[type][v], dp[type ^ 1][to] + weight);
Thus, we choose
the best next move that leads to the maximum total path length. This is
analogous to the standard longest path search in a DAG (directed acyclic
graph), where the direction of edges is determined by the decrease in shortest
distance.
Movement is
allowed only along edges leading to vertices with a smaller distance to
Domnino. However, the problem involves two graphs – two types of edges: roads
and trails – and transitions between them alternate: night (road), day (trail),
night, day, and so on. It is precisely because of this alternation of maps
(roads and trails) that a cycle may arise between vertices, even though in each
individual graph (for one map) the movement always goes along decreasing
distances.
If during the
depth-first search we encounter a vertex that is already in the processing
stack, it means a cycle has been detected.
Algorithm implementation
Declare the constants.
#define INF 2e18
#define MAXN 1005
Let’s declare the data structures used:
·
g[0] and g[1] – adjacency lists for the road and trail graphs,
respectively.
·
d[0] and d[1] – shortest distances from the village Domnino t
to all other villages.
·
dp[0] and dp[1] – the maximum path length from vertex v to t, if starting from v along the road (type
= 0) or
along the trail (type = 1).
·
used[0] and used[1] – vertex visitation
markers for depth-first search in the road and trail graphs, respectively.
vector<pair<int, int>> g[2][MAXN];
long long d[2][MAXN];
long long dp[2][MAXN];
int used[2][MAXN];
The function dijkstra
calculates the shortest distances from the village Domnino t to all
other villages either along the roads (type = 0) or along the trails (type
= 1).
void dijkstra(int type)
{
for (int i = 1; i <= n; i++)
d[type][i] = INF;
d[type][t] = 0;
priority_queue<pair<long long, int>, vector<pair<long long, int>>, greater<pair<long long, int>>> pq;
pq.push({ 0, t });
while (!pq.empty())
{
pair<long long, int> top = pq.top();
pq.pop();
long long dist = top.first;
int v = top.second;
if (dist > d[type][v]) continue;
for (auto edge : g[type][v])
{
int to = edge.first;
int w = edge.second;
if (d[type][to] > d[type][v] + w)
{
d[type][to] = d[type][v] + w;
pq.push({ d[type][to], to });
}
}
}
}
The dfs function performs a depth-first search and
finds the longest path while moving through alternating maps, starting from
village v along the road (type = 0) or along the trail (type
= 1). If during such alternating movement a cycle is detected, the function
returns -1.
void dfs(int v, int type)
{
Vertex v
in the graph g[type] is marked as gray.
used[type][v] = 1;
Initialize
the dynamic programming state.
dp[type][v] = 0;
Iterate
over the edges outgoing from vertex v in the graph g[type].
for (auto edge : g[type][v])
{
int to = edge.first;
int weight = edge.second;
A
transition from vertex v to vertex to is allowed only if the
distance from to to Domnino is less than the
distance from v to Domnino.
if (d[type][to] < d[type][v])
{
If the
vertex to in the graph g[type ^ 1] is
already in the process of being visited (marked as “gray”), then a cycle has
been detected – return -1.
if (used[type ^ 1][to] == 1)
{
cout << -1 << endl;
exit(0);
}
If the
vertex to in the graph g[type ^ 1] has
not yet been visited, continue the depth-first search from it.
if (used[type ^ 1][to] == 0)
dfs(to, type ^ 1);
After
processing all allowed transitions, update the dynamic programming state by
selecting the maximum path length from vertex v in the graph g[type] to Domnino.
dp[type][v] = max(dp[type][v], dp[type ^ 1][to] + weight);
}
}
Vertex v
in the graph g[type] is marked black.
used[type][v] = 2;
}
The main part of the program. Read the input data and construct the road
and trail graphs.
scanf("%d %d %d", &n, &s, &t);
scanf("%d", &m1);
for (i = 0; i < m1; i++)
{
scanf("%d %d %d", &a, &b, &len);
g[0][a].push_back({ b, len });
g[0][b].push_back({ a, len });
}
scanf("%d", &m2);
for (i = 0; i < m2; i++)
{
scanf("%d %d %d", &a, &b, &len);
g[1][a].push_back({ b, len });
g[1][b].push_back({ a, len });
}
Calculate the
shortest distances from the village Domnino t to all other villages – separately
for the road map and for the trail map.
dijkstra(0);
dijkstra(1);
Using depth - first search, find the longest path while moving through
alternating maps, starting from the village s along the road.
dfs(s, 0);
Print the answer. The starting point is village s, and the movement
begins on the road.
printf("%lld\n", dp[0][s]);