2268. Кухонный робот

Роботы со временем становятся всё популярнее. Сегодня их применяют не только на крупных заводах, но и в быту. Один программист вместе с друзьями решил создать собственного домашнего робота. Как вы знаете, большинство программистов любит собираться на вечеринки и пить пиво. После таких вечеринок на столе остаётся множество пустых бутылок. Поэтому было решено разработать робота, способного собирать пустые бутылки со стола.

Стол представляет собой прямоугольник длиной l и шириной w. Робот начинает движение из точки (x_r, y_r), а n бутылок расположены в точках (x_i, y_i) (1 ≤ i ≤ n). Чтобы забрать бутылку, робот должен переместиться в точку её расположения, взять её, а затем отнести в некоторую точку на границе стола и отпустить. В каждый момент времени робот может держать только одну бутылку и может отпускать её только на границе стола.

Размеры бутылок и робота считайте пренебрежимо малыми (и робот, и бутылки являются точками). Робот, держащий бутылку, может проходить через точки, в которых находятся другие бутылки.

Одной из подпрограмм робота является планирование маршрута. Вам требуется написать программу, которая определяет маршрут минимальной длины, по которому робот соберёт все бутылки.

Вход. Первая строка содержит два целых числа w и l (2 ≤ w, l ≤ 1000) – ширина и длина стола.

Вторая строка содержит количество бутылок n (1 ≤ n ≤ 18). Каждая из следующих n строк содержит два целых числа x_i и y_i (0 < x_i < w, 0 < y_i < l) – координаты i-ой бутылки. Никакие две бутылки не находятся в одной точке.

Последняя строка содержит два целых числа x_r и y_r (0 < x_r < w, 0 < y_r < l) – координаты начального положения робота.  Робот не расположен в одной точке ни с одной бутылкой.

Выход. Выведите длину кратчайшего пути, по которому робот соберёт все бутылки. Погрешность вычислений не должна превышать 10^-6.

Пример входа	Пример выхода
3 4 2 1 1 2 3 2 1	5.60555127546399

РЕШЕНИЕ

динамическое программирование - задача коммивояжера, NP полнота

Анализ алгоритма

Пусть A и B – две бутылки, которые робот будет собирать последовательно. После того как робот поднимет бутылку A, он должен отнести её к одной из четырёх границ стола и выбросить. Лишь затем робот может направиться за бутылкой B. Найдём кратчайший путь робота от точки A(x_i, y_i) до точки B(x_j, y_j) с обязательным заходом на край стола.

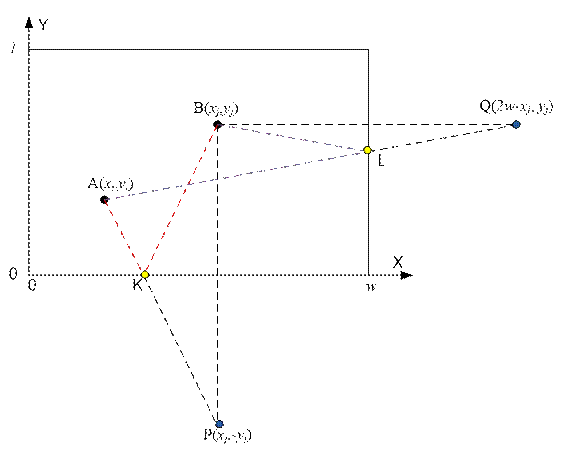
Расстояние AK + KB = AK + KP = AP. Зная координаты точек A(x_i, y_i) и P(x_j, -y_j), можно вычислить расстояние

AP = =

Расстояние AL + LB = AL + LQ = AQ. Абсцисса точки Q равна w + (w – x_j) = 2w – x_j. Зная координаты точек A(x_i, y_i) и Q(2w – x_j, y_j), можно вычислить расстояние

AQ =

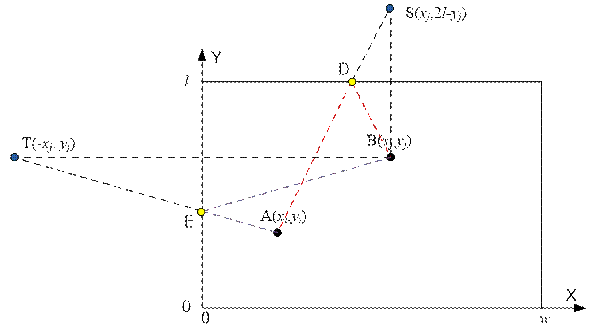
Расстояние AE + EB = AE + ET = AT. Зная координаты точек A(x_i, y_i) и T(-x_j, y_j), можно вычислить расстояние

AT = =

Расстояние AD + DB = AD + DS = AS. Ордината точки S равна l + (l – y_j) = 2l – y_j. Зная координаты точек A(x_i, y_i) и S(x_j, 2l – y_j), можно вычислить расстояние

AS =

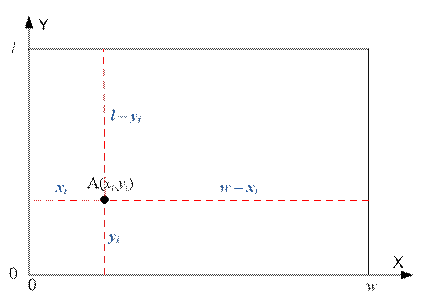
Найдём наименьшее расстояние, которое необходимо пройти роботу, чтобы выбросить бутылку, расположенную в точке (x_i, y_i), за край стола. Это расстояние равно минимуму из четырёх значений:

min( x_i, y_i, w – x_i, l – y_i)

Именно такой путь робот должен будет пройти, чтобы выбросить последнюю бутылку.

Начальное положение робота и координаты всех бутылок заданы. Рассмотрим граф, в котором нулевая вершина соответствует начальному положению робота, а остальные вершины – бутылкам. Расстояние между нулевой вершиной и каждой из остальных определяется как Евклидово расстояние между соответствующими точками. Расстояние между бутылками i и j задаётся как минимальный путь, который робот должен пройти от бутылки i до бутылки j, обязательно побывав на границе стола. Поскольку на столе находится n бутылок, граф будет содержать n + 1 вершину.

Далее необходимо найти в этом графе Гамильтонов путь минимальной длины. После того как робот дойдёт до последней бутылки, к общей длине пути нужно добавить расстояние, необходимое для выбрасывания этой бутылки за край стола. Поиск Гамильтонова пути выполняется с помощью динамического программирования по маскам, с асимптотической сложностью O(n² * 2ⁿ).

Пример

Ниже приведены начальное положение робота и координаты бутылок.

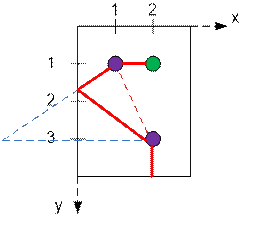
Длина кратчайшего пути робота равна

1 + + 1 = 2 + ≈ 5.605

Реализация алгоритма

Объявим константу INF, обозначающую бесконечность, и константу MAX – максимальное количество точек в Гамильтоновом пути.

#define INF 1e18

#define MAX 20

Объявим массив dp, в котором будут храниться значения dp(S, i), пересчитываемые динамически. Координаты бутылок сохраняем в точках (x_i, y_i) (1 ≤ i ≤ n). Начальное положение робота храним в точке (x₀, y₀).

double dp[1 << MAX][MAX + 1];

double x[MAX], y[MAX], m[MAX][MAX];

Функция solve вычисляет значение dp(S, last) – минимальное расстояние, чтобы пройти по всем точкам из множества S, закончив на вершине last. Множество S кодируется целым числом mask. Тогда:

dp(S, last) = ,

где

· m[i][last] – расстояние между точками i и last,

· S \ {last} = mask ^ (1<< last) – множество S без элемента last.

Переменная res соответствует ячейке dp[mask][last], поэтому при изменении res автоматически обновляется и значение dp[mask][last].

double solve(int mask, int last)

{

double &res = dp[mask][last];

if (res == INF)

{

mask ^= (1 << last);

for (int i = 1; i < n; i++)

if ((mask & (1 << i)) && (i != last))

res = min(res, solve(mask, i) + m[i][last]);

}

return res;

}

Функция f возвращает кратчайшее расстояние от точки (x[i], y[i]) до границы стола.

double f(int i)

{

return min(min(x[i], y[i]), min(l - y[i], w - x[i]));

}

Функция dist возвращает расстояние между точками (x[i], y[i]) и (x[j], y[j]).

double dist(int i, int j)

{

return sqrt((x[i] - x[j])*(x[i] - x[j]) +

(y[i] - y[j])*(y[i] - y[j]));

}

Основная часть программы. Читаем размер стола w и l.

scanf("%d %d", &w, &l);

Читаем количество бутылок n и их координаты (x[i], y[i]).

scanf("%d", &n);

for (i = 1; i <= n; i++)

scanf("%lf %lf", &x[i], &y[i]);

Начальные координаты робота сохраняем в (x[0], y[0]).

scanf("%lf %lf", &x[0], &y[0]);

К n бутылкам добавляем нулевую вершину, соответствующую начальному положению робота. После этого n увеличивается на единицу и становится равным общему числу вершин в графе. Вершины графа нумеруются от 0, 1, …, n – 1.

n++;

Вычисляем попарные расстояния между бутылками. Расстояние между бутылками i и j определяется как минимальный путь, который робот должен пройти от бутылки i до бутылки j с обязательным заходом на границу стола.

for (i = 1; i < n - 1; i++)

for (j = i + 1; j < n; j++)

m[i][j] = m[j][i] =

min(

min(sqrt((x[i] + x[j])*(x[i] + x[j]) + (y[i] - y[j])*(y[i] - y[j])),

sqrt((2 * w - x[i] - x[j])*(2 * w - x[i] - x[j]) +

(y[i] - y[j])*(y[i] - y[j]))),

min(sqrt((x[i] - x[j])*(x[i] - x[j]) + (y[i] + y[j])*(y[i] + y[j])),

sqrt((x[i] - x[j])*(x[i] - x[j]) +

(2 * l - y[i] - y[j])*(2 * l - y[i] - y[j])))

);

Изначально значения dp(S, i) неизвестны, поэтому присваиваем им значение плюс бесконечность.

for (i = 0; i < 1 << n; i++)

for (j = 0; j < n; j++)

dp[i][j] = INF;

Множеству {0} соответствует маска 1. Установим dp({0}, 0) = 0, так как минимальный путь из нулевой вершины в саму себя без посещения других вершин равен нулю. В переменной total будем хранить искомую минимальную длину Гамильтонова пути.

dp[1][0] = 0; total = INF;

for (i = 1; i < n; i++) dp[1 | (1 << i)][i] = dist(0, i);

Находим Гамильтонов путь минимальной длины. Значение 2ⁿ – 1 соответствует множеству всех вершин {0, 1, 2, ..., n – 1}. Вычисляем минимум среди всех значений:

dp({0, 1, 2, ..., n – 1}, i) + f(i), 1 £ i < n

После нахождения минимальной длины Гамильтонова пути к результату нужно добавить расстояние, которое робот проходит, чтобы выбросить последнюю i-ую бутылку за границу стола – оно равно f(i).

for (i = 1; i < n; i++)

total = min(total, solve((1 << n) - 1, i) + f(i));

Выводим искомую минимальную длину пути.

printf("%.6lf\n", total);