2268. Kitchen Robot
Robots are
becoming increasingly popular over time. Today, they are used not only in large
factories but also in everyday household settings. One programmer, together
with his friends, decided to create a home robot of their own. As you may know,
many programmers enjoy attending parties and drinking beer. After such parties,
the table is usually left covered with empty bottles. Therefore, they decided
to develop a robot capable of collecting empty bottles from the table.
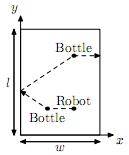
The table is a
rectangle of length l and width w. The robot starts at point (xr, yr), and n bottles are located at points (xi,
yi)
(1 ≤ i ≤ n). To pick up a bottle, the
robot must move to its location, grab it, then carry it to some point on the
table boundary and release it. At any moment, the robot can hold only one
bottle and may release it only at the boundary of the table.
The sizes of the
bottles and the robot can be considered negligible (both the robot and the
bottles are treated as points). A robot holding a bottle may pass through
points where other bottles are located.
One of the
robot’s subprograms is route planning. You are required to write a program that
determines the shortest possible route by which the robot can collect all the
bottles.
Input. The first line contains two integer
numbers w
and l (2 ≤ w, l ≤ 1000) – the width and
the length of the table.
The second line
contains the number of bottles n (1 ≤ n
≤ 18). Each of the next n lines
contains two integers xi and yi (0
< xi < w, 0 < yi < l) – the coordinates of the i-th bottle. No two bottles are located
at the same point.
The last line
contains two integers xr and yr (0 < xr < w, 0 < yr < l) – the
coordinates of the robot’s starting position. The robot does not share a point
with any bottle.
Output. Print the length of the shortest route by which the robot collects
all the bottles. The computation error must not exceed 10-6.
|
Sample input |
Sample output |
3 421 12 3
2 1 |
5.60555127546399 |
SOLUTION
dynamic programming – TSP problem
Algorithm analysis
Let A and B be two bottles
that the robot will pick up sequentially. After the robot picks up bottle A, it
must carry it to one of the four edges of the table and dispose of it. Only
then may the robot proceed to bottle B. We need to find the shortest path for
the robot from point A(xi,
yi) to point B(xj, yj), with a mandatory visit to the table’s edge.
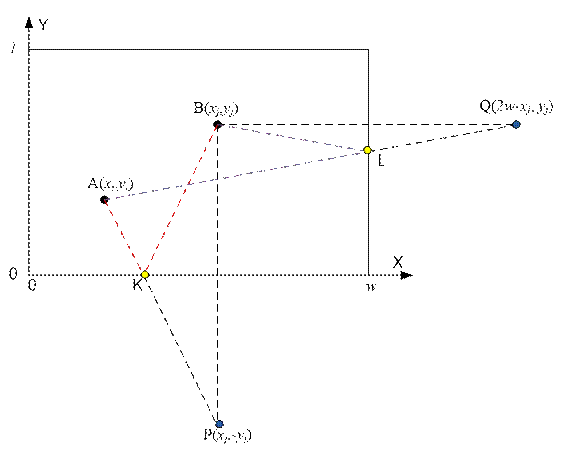
The distance AK + KB = AK
+ KP = AP. Knowing the coordinates of points A(xi, yi) and P(xj, -yj),
we can compute this distance:
AP = ![]() =
= ![]()
The distance AL + LB = AL
+ LQ = AQ. The x-coordinate of point Q equals w + (w – xj) = 2w – xj. Knowing the coordinates of
points A(xi, yi) and Q(2w – xj, yj), we can compute this
distance:
AQ = ![]()
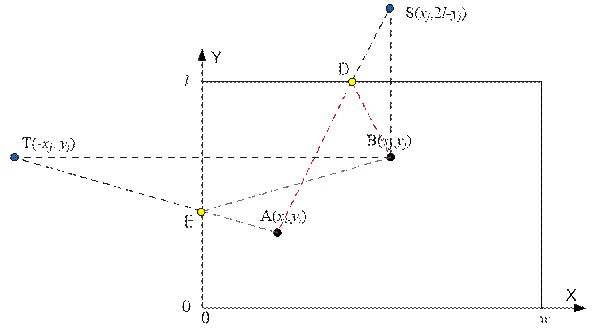
The distance AE + EB = AE + ET = AT. Knowing the
coordinates of points A(xi,
yi) and T(-xj, yj),
we can compute this distance:
AT = ![]() =
= ![]()
The distance AD + DB = AD + DS = AS. The y-coordinate
of point S equals l + (l – yj) = 2l – yj. Knowing the coordinates of
points A(xi, yi) and S(xj, 2l – yj), we can compute this
distance:
AS = ![]()
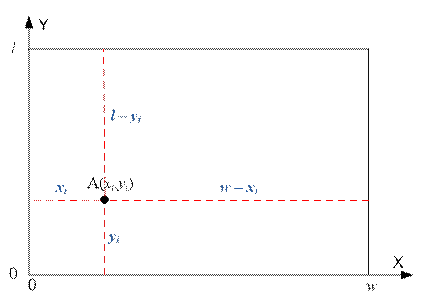
Let us find the minimum
distance the robot must travel to throw away the bottle located at point (xi, yi) over the edge of the
table. This distance is equal to the minimum of the four values:
min( xi, yi, w – xi,
l – yi)
This is exactly the path
the robot will have to take to dispose of the last bottle.
The initial position of
the robot and the coordinates of all bottles are given. Consider a graph where
vertex 0 corresponds to the robot’s starting position, and the remaining
vertices correspond to the bottles. The distance between vertex 0 and any other
vertex is defined as the Euclidean distance between the corresponding points.
The distance between bottles i and j is defined as the minimum
path the robot must travel from bottle i to bottle j, with the
requirement that it must touch the edge of the table. Since there are n bottles
on the table, the graph will contain n + 1 vertices.
Next, we need to find a
Hamiltonian path of minimum length in this graph. After the robot reaches the
last bottle, we must add the distance required to throw this bottle off the
edge of the table to the total path length. The Hamiltonian path is computed
using dynamic programming over subsets, with a time complexity of O(n2 * 2n).
Below are the robot’s initial position and
the coordinates of the bottles.
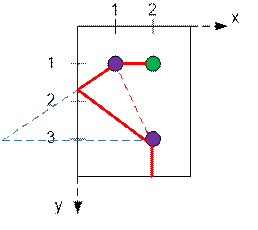
The length of
the robot’s shortest path is
1 + ![]() +
1 = 2 +
+
1 = 2 + ![]() ≈ 5.605
≈ 5.605
Algorithm implementation
Let’s define the constant
INF to represent infinity, and the constant MAX as the maximum number of points
in the Hamiltonian path.
#define INF 1e18
#define MAX 20
Declare
an array dp that will store the values dp(S, i), which are computed
dynamically. The coordinates of the bottles are stored as points (xi, yi) (1
≤ i ≤ n). The robot’s initial position is stored
at the point (x0, y0).
double dp[1 << MAX][MAX +
1];
double x[MAX], y[MAX], m[MAX][MAX];
The function solve computes the value dp(S, last)
– the minimum distance required to visit all points in the set S, finishing at
the vertex last. The set S is encoded by an integer mask. Then:
dp(S, last) = ![]() ,
,
where
·
m[i][last] is the distance between
points i and last,
·
S \ {last} = mask ^
(1<< last) is the set S without the element last.
The variable res corresponds to the cell dp[mask][last],
so when res is updated, the value of dp[mask][last] is
automatically updated as well.
double solve(int mask, int last)
{
double
&res = dp[mask][last];
if (res
== INF)
{
mask ^=
(1 << last);
for (int i =
1; i < n; i++)
if ((mask
& (1 << i)) && (i != last))
res = min(res, solve(mask, i) + m[i][last]);
}
return res;
}
The
function f returns the shortest distance
from the point (x[i], y[i]) to the edge of the table.
double f(int i)
{
return
min(min(x[i], y[i]), min(l - y[i], w
- x[i]));
}
The
function dist returns the distance
between the points (x[i], y[i]) and (x[j], y[j]).
double dist(int i, int j)
{
return
sqrt((x[i] - x[j])*(x[i] -
x[j]) +
(y[i] -
y[j])*(y[i] - y[j]));
}
The
main part of the program. Read the table dimensions w and l.
scanf("%d %d",
&w, &l);
Read
the number of bottles n and their coordinates (x[i], y[i]).
scanf("%d", &n);
for (i = 1; i <= n; i++)
scanf("%lf %lf",
&x[i], &y[i]);
The
robot’s initial coordinates are stored in (x[0], y[0]).
scanf("%lf %lf", &x[0], &y[0]);
We
add a zero vertex to the n bottles,
corresponding to the robot’s initial position. After that, n is
increased by one and becomes the total number of vertices in the graph. The
graph vertices are numbered 0, 1, …, n – 1.
n++;
Let’s
compute all pairwise distances between the bottles. The distance between
bottles i and j is defined as the minimum path the robot must
travel from bottle i to bottle j, with the requirement that it
must touch the edge of the table.
for (i = 1; i < n - 1; i++)
for (j = i + 1; j < n; j++)
m[i][j]
= m[j][i] =
min(
min(sqrt((x[i]
+ x[j])*(x[i] + x[j]) + (y[i] - y[j])*(y[i] - y[j])),
sqrt((2
* w - x[i] - x[j])*(2 * w - x[i] - x[j]) +
(y[i] - y[j])*(y[i] - y[j]))),
min(sqrt((x[i] - x[j])*(x[i] - x[j]) +
(y[i] + y[j])*(y[i] + y[j])),
sqrt((x[i]
- x[j])*(x[i] - x[j]) +
(2 * l - y[i] - y[j])*(2 * l - y[i] - y[j])))
);
Initially,
the values of dp(S, i) are unknown, so we assign them positive infinity.
for (i = 0; i < 1 << n; i++)
for (j = 0; j < n; j++)
dp[i][j]
= INF;
The
set {0} corresponds to the mask 1. Set dp({0}, 0) = 0, since the minimum path from the
zero vertex to itself without visiting other vertices is zero. The variable total will store the required minimum
length of the Hamiltonian path.
dp[1][0] = 0; total
= INF;
for (i = 1; i < n;
i++) dp[1 | (1 << i)][i] = dist(0, i);
Find the Hamiltonian path of
minimum length. The value 2n – 1 corresponds to the set of all vertices {0, 1, 2, ..., n –
1}. Compute the
minimum among all values:
dp({0, 1, 2,
..., n – 1}, i) + f(i), 1 £ i < n
After obtaining the minimum
length of the Hamiltonian path, we must add the distance the robot needs to
travel to throw the final bottle i off the edge of the table – this
distance is f(i).
for (i = 1; i < n;
i++)
total = min(total, solve((1 << n) - 1, i) + f(i));
Print
the required minimum path length.
printf("%.6lf\n",
total);