2270. Find a cycle
You are given a
directed unweighted graph. Determine whether it
contains any cycles. If the graph contains a cycle, print any one of them.
Input. The first line
contains two positive integers n and m (1 ≤ n ≤ 105, 1 ≤ m ≤ 105) – the number of vertices and edges in the
graph, respectively. The next m lines list the
edges of the graph. Each edge is defined by a pair of numbers representing the
starting and ending vertices.
Output. If the graph does
not contain any cycles, print the string “NO”. If a cycle exists, print the
string “YES”, followed by the vertices that form the cycle in the order they
are traversed. If there are multiple cycles, print any one of them.
|
Sample
input 1 |
Sample
output 1 |
2 21 2
2 1 |
YES 1 2 |
|
|
|
|
Sample
input 2 |
Sample
output 2 |
|
6 7 1 2 2 3 2 4 4 6 6 5 1 5 5 2 |
YES 2 4 6 5 |
SOLUTION
graphs – depth first
search
Algorithm analysis
Perform a series
of depth-first searches (DFS) on the graph. For this, start a DFS from each
vertex that is not visited yet. Upon entering a vertex, color it gray,
and upon exiting, color it black. If during the search we attempt to
move to a vertex that is already colored gray, it means a cycle is detected.
To restore the
cycle, it is necessary to store the sequence of vertices in the order they are
traversed. For example, if the traversal array contains the vertices (2, 6, 3,
5, 4, 3), the desired cycle will be (3, 5, 4).
Example
The graphs given
in the problem statement have the following structure:
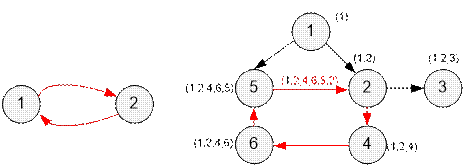
Next to each
vertex, the current state of the path array is indicated.
Algorithm implementation
The adjacency
list of the graph is stored in the vector g. The path array
stores the sequence of vertices in the order they are traversed during the
depth-first search.
vector<vector<int> > g;
vector<int> used, path;
The function dfs implements a
depth-first search starting from vertex v. Upon entering vertex v,
color it gray (used[v] = 1), and upon
exiting, color it black (used[v] = 2).
The global variable flag indicates the presence of a cycle: flag = 1 means a cycle is found, flag = 0 means there is no cycle.
void dfs(int
v)
{
If a cycle is
found (flag = 1), there is no point
in continuing the search.
if
(flag == 1) return;
Mark vertex v as gray and add it to the path
array.
used[v] = 1;
path.push_back(v);
Iterate over the vertices to, adjacent to v.
for (int to : g[v])
A cycle is
considered found if the depth-first search tries to move to a gray vertex (a
vertex to for which used[to] = 1).
if
(used[to] == 1)
{
path.push_back(to);
flag = 1;
return;
}
If vertex to is still white, continue the
depth-first search from it.
else
{
if (used[to] == 0) dfs(to);
if (flag == 1) return;
}
}
After finishing
the processing of vertex v, mark it as black. Remove vertex v
from the path array.
used[v] = 2;
path.pop_back();
}
The main part of
the program. Read the list of edges and build the adjacency list of the graph.
scanf("%d %d", &n, &m);
g.resize(n + 1);
used.resize(n + 1, 0);
for(i = 0; i < m; i++)
{
scanf("%d
%d",&a,&b);
g[a].push_back(b);
}
Start a series of
depth-first searches. If vertex i is not processed yet (used[i] =
0, start a depth-first search from it. If during the execution of the next dfs
function call the value of the variable flag becomes 1 (a cycle is
detected in the graph), we stop further searching.
for (i = 1; i <= n; i++)
if
(used[i] == 0)
{
dfs(i);
if
(flag == 1) break;
}
If flag = 1, it means that a cycle is
found. In this case, print it based on the information in the path
array.
if (flag == 1)
{
The cycle is found and ends at vertex cfin =
path[path.size() – 1].
cfin = path.back();
Move the variable
cstart backwards through the path array to find the same vertex cfin
– the point where the cycle starts.
cstart = path.size() - 2;
while (path[cstart] != cfin) cstart--;
Print a message indicating the presence of a cycle and the
cycle itself.
printf("YES\n");
for (i = cstart; i < path.size() - 1; i++)
printf("%d ", path[i]);
printf("\n");
}
Otherwise (flag = 0), there are no cycles in the graph.
else printf("NO\n");
Java implementation
import java.util.*;
public class Main
{
static
ArrayList<Integer>[] g;
static int used[], flag, n, m;
static Vector<Integer> path = new
Vector<Integer>();
static void dfs(int v)
{
if (flag == 1) return;
used[v] = 1;
path.add(v);
for (int i = 0; i < g[v].size(); i++)
{
int to = g[v].get(i);
if (used[to] == 1)
{
path.add(to);
flag = 1;
return;
}
else dfs(to);
if (flag == 1) return;
}
used[v] = 2;
path.remove(path.size() - 1);
}
public static void main(String[] args)
{
Scanner
con = new Scanner(System.in);
n = con.nextInt();
m = con.nextInt();
g = new ArrayList[n+1];
for (int i = 0; i <= n; i++)
g[i] = new ArrayList<Integer>();
used = new int[n+1];
for(int i = 0; i < m; i++)
{
int a = con.nextInt();
int b = con.nextInt();
g[a].add(b);
}
for (int i = 1; i <= n; i++)
if (used[i] == 0)
{
dfs(i);
if (flag == 1) break;
}
if (flag == 1)
{
int i = path.size() - 2;
int to = path.lastElement();
while (path.get(i) != to) i--;
System.out.println("YES");
for (; i < path.size() - 1; i++)
System.out.print(path.get(i) + " ");
System.out.println();
}
else System.out.println("NO");
con.close();
}
}