2299. Теодор Рузвельт

"Теодор Рузвельт" – флагман военно-морского флота Кукуляндии. Заклятые враги кукуляндцев, флатландцы, решили уничтожить его. Они узнали, что "Теодор Рузвельт" представляет собой выпуклый многоугольник из n вершин и узнали его координаты. Затем они выпустили m баллистических ракет и определили координаты точек, где эти ракеты взорвались. По расчетам штаба флатландцев, "Теодор Рузвельт" будет уничтожен, если в него попадёт хотя бы k ракет. Вычислите, удалось ли флатландцам уничтожить корабль.

Вход. В первой строке записаны целые числа n, m, k (3 ≤ n ≤ 10⁵, 0 ≤ k ≤ m ≤ 10⁵). В следующих n строках записаны координаты вершин многоугольника в порядке обхода против часовой стрелки. В следующих m строках записаны координаты точек. Гарантируется, что все координаты – целые числа, не превосходящие по модулю 10⁹.

Выход. Выведите YES, если в многоугольнике лежит по крайней мере k точек, и NO в противном случае.

Пример входа	Пример выхода
5 4 2 1 -1 1 2 0 4 -1 2 -1 -1 -2 -1 1 -1 0 1 2 3	YES

РЕШЕНИЕ

геометрия + бинарный поиск

Анализ алгоритма

Рассмотрим, как решить задачу принадлежности точки выпуклому многоугольнику.

Координаты вершин многоугольника заданы в порядке обхода против часовой стрелки: p₁, p₂, …, p_n. Рассмотрим первую точку многоугольника p₁. Относительно нее все остальные точки будут отсортированы по углу. Проведём от точки p₁ все лучи, содержащие диагонали. Бинарным поиском ищем такое ребро p_ip_i+1, что повороты p₁p_iq и p₁p_i+1q различны. Таким образом мы найдем область, в которой лежит точка q.

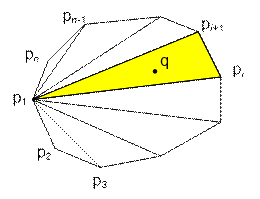
Когда найден угол p_ip₁p_i+1, в котором находится точка q, за константное время можно проверить, с одной ли стороны от прямой p_ip_i+1 лежат точки p₁ и q. Для этого поворот p_ip_i+1q должен быть левым (поворот p_ip_i+1p₁ является левым, так как исходные точки многоугольника заданы в порядке обхода против часовой стрелки).

В начале алгоритма следует проверить, не является ли поворот p₁p_nq левым, или поворот p₁p₂q правым. Если выполняется хотя бы одно из этих условий, то q лежит вне многоугольника.

Направление поворота. Пусть совершается движение от точки А до В, затем от В до С. При движении имеет место левый поворот (движение происходит против часовой стрелки), если AB ´ BC > 0 (псевдоскалярное произведение векторов положительно) и правый, если AB ´ BC < 0.

Реализация алгоритма

Объявим структуру точка и массив точек.

#define MAX 100001

struct Point

{

long long x, y;

Point(long long x = 0, long long y = 0) : x(x), y(y) {}

};

Point p[MAX];

Функция angle определяет левый или правый поворот происходит при движении по точкам А , B, С. Вычислим вектора:

AB = (b.x – a.x, b.y – a.y)

BC = (c.x – b.x, c.y – b.y)

Псевдоскалярное произведение AB x BC равно

= (b.x – a.x) * (c.y – b.y) – (b.y – a.y) * (c.x – b.x)

и его знак определяет направление поворота:

· положительный – левый поворот;

· отрицательный – правый поворот;

int angle(Point a, Point b, Point c)

{

long long q = (b.x - a.x) * (c.y - b.y) - (b.y - a.y) * (c.x - b.x);

return (q > 0) - (q < 0); // sgn(q)

}

Функция inside возвращает true, если точка q лежит внутри многоугольника.

bool inside(Point q)

{

Первую точку выберем базовой.

Point a = p[1];

Если поворот p₁p_nq левый, или поворот p₁p₂q правый, то точка q лежит вне угла p_np₁p₂ и соответственно вне многоугольника.

if (angle(a, p[2], q) < 0 || angle(a, p[n], q) > 0) return false;

Стартуем бинарный поиск на отрезке [l; r] = [2; n]. Ищем такие точки p_l и p_r (r = l + 1) что точка q лежит внутри угла p_lp₁p_r.

int l = 2, r = n, m;

while (l + 1 < r)

{

m = (l + r) / 2;

if (angle(a, p[m], q) < 0)

r = m;

else

l = m;

}

return angle(p[l], p[r], q) >= 0;

}

Основная часть программы. Читаем входные данные.

scanf("%d %d %d", &n, &m, &k);

for (int i = 1; i <= n; i++)

{

scanf("%lld %lld", &x, &y);

p[i] = Point(x, y);

}

Вычисляем количество точек, лежащих внутри многоугольника.

res = 0;

for (int i = 1; i <= m; ++i)

{

scanf("%lld %lld", &x, &y);

if (inside(Point(x, y))) res++;

}

Выводим ответ.

if (res < k) puts("NO"); else puts("YES");