2302. Орехи для орехов
Райан и Ларри
решили, что их орехи не слишком приятны на вкус. Однако имеется несколько
орехов, расположенных в некоторых местах острова, и они очень вкусные! Но
поскольку ребята ленивые и жадные, то они хотят знать кратчайший путь, по
которому можно собрать все орехи. Можете ли Вы им помочь?
Вход. Первая строка каждого теста содержит размеры
прямоугольного острова x и y (x, y ≤ 20). Далее следуют x строк по y символов, описывающие карту местности. Она состоит из символов ‘.’,
‘#’ и ‘L’. Изначально Ларри и Райан находятся в ‘L’, орехи обозначаются
символами ‘#’. Ребята за один шаг могут попасть в любую из восьми соседних
клеток. Количество клеток, в которых могут располагаться орехи, не более 15.
Клетка с символом ‘L’ на карте всего одна.
Выход. Для каждой
карты в отдельной строке вывести наименьшее количество шагов, за которое
стартовав с клетки ‘L’, можно собрать все орехи, и вернуться в ‘L’.
|
Пример
входа |
Пример
выхода |
|
5 5 L.... #.... #.... ..... #.... 8 10 L......... .......... .......#.. .......... #....#.... .........# .......... ....#..... |
8 23 |
РЕШЕНИЕ
динамическое
программирование - задача коммивояжера, NP полнота
Анализ алгоритма
Это
классическая задача коммивояжера. Следует найти цикл минимальной длины,
проходящий по всем вершинам графа. Или то же самое что найти гамильтонов цикл
минимальной длины. Задача является NP полной и требует экспоненциального
времени для ее решения относительно числа вершин в графе.
Пусть n – число вершин в графе. Каждому ореху и
начальному местоположению Лари поставим в соответствие вершину графа. Из
условия задачи следует, что n £ 16. Все вершины
графа будут попарно соединены (решается евклидова задача коммивояжера). Длина
ребра, соединяющего вершины которым соответствуют координаты (a, b)
и (c, d), равна max( |a – c|, |b – d|
). Матрицу смежности построенного графа храним в двумерном массиве m.
Можно
сгенерировать при помощи функции next_permutation все возможные
перестановки чисел от 1 до n, каждой перестановке будет соответствовать
гамильтонов цикл. Ищем минимальное значение среди всех длин таких циклов.
Приведенный алгоритм требует n! времени, что для n = 16 слишком
много (следует перебрать 16! = 20922789888000 вариантов).
Используя метод
динамического программирования, можно решить задачу с оценкой O(2n)
по используемой памяти и O(n2 * 2n) по
времени работы алгоритма. При n = 16 следует перебрать 16777216
вариантов, что реально по времени.
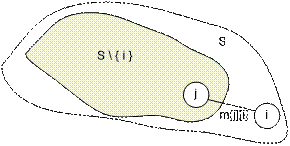
Для непустого подмножества S Í {1, 2, …, n}
и каждой вершины i Î S определим
dp(S, i) как длину кратчайшего пути, начинающегося в первой (начальной)
вершине, проходящего по всем вершинам из множества S \ {i} в
произвольном порядке и оканчивающегося в вершине i. Тогда имеют место
равенства:
dp({1, i}, i) = m[1][i],
dp(S, i) = ![]() (dp(S \ {i}, j) + m[j, i] )
(dp(S \ {i}, j) + m[j, i] )
Значения dp(S, i)
пересчитываем динамически, запоминая их в массиве dp. Гамильтонов цикл
минимальной длины равен
![]() (dp({1, 2, ..., n}, j) + m[j, 1] )
(dp({1, 2, ..., n}, j) + m[j, 1] )
Пример
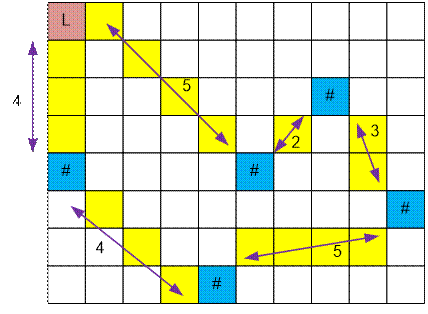
В первом тесте
достаточно пройти вниз острова (4 шага), собрав по пути все орехи, и подняться наверх
к исходному месту (еще 4 шага).
Рассмотрим второй
тест. Пять орехов и начальное положение Ларри образуют граф из 6 вершин. На
рисунке изображен гамильтонов путь длины 23.
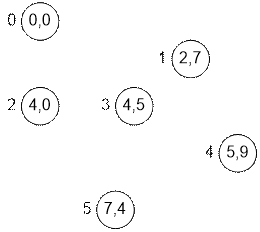
Рассмотрим процесс вычислений более подробно. В каждой вершине
указана (x, y)
координата
ореха, которому она соответствует. Возле каждой вершины указан ее номер.
Инициализируем dp({0, i}, i) = m[0][i]
(вершина 0 – местоположение Лари):
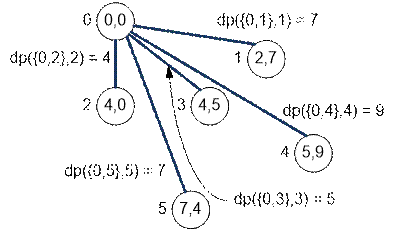
Вершина 0 в маске соответствует младшему биту. Равенство
dp({0, i}, i) = m[0][i] эквивалентно dp(2i
+ 1, i) = m[0][i], так как множеству {0, i} соответствует
маска 2i + 1.
Рассмотрим
гамильтоновы пути по первым трем вершинам, если путь завершается в вершине 1
(слева) или в вершине 2 (справа).
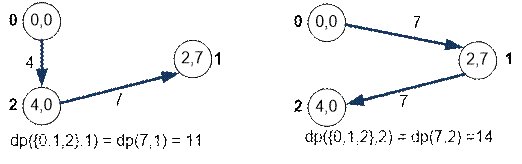
Найдем
минимальную длину гамильтонова пути по первым четырем вершинам, который
завершается в вершине 3:
dp({0, 1, 2, 3},
3) = min(dp({0, 1, 2}, 1) + m[1][3], dp({0, 1, 2}, 2) + m[2][3]) =
min(11 + 2, 14 + 5) =
min(13, 19) = 13
Минимум
достигается на слагаемом dp({0, 1, 2}, 1) + m[1][3], следовательно
наилучшим путем будет
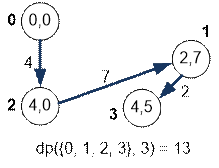
Рассмотрим
гамильтоновы пути по вершинам {0, 1, 3}, если путь завершается в вершине 1 (слева) или в вершине 3 (справа).
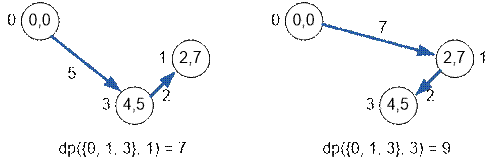
Найдем
минимальную длину гамильтонова пути по первым четырем вершинам, который
завершается в вершине 2:
dp({0, 1, 2, 3},
2) = min(dp({0,
1, 3}, 1) + m[1][2], dp({0, 1, 3}, 3) + m[3][2]) =
min(7 + 7, 9 + 5) = min(14,
14) = 14
Минимум
достигается на обоих слагаемых, следовательно имеется два гамильтоновых пути
одной длины:
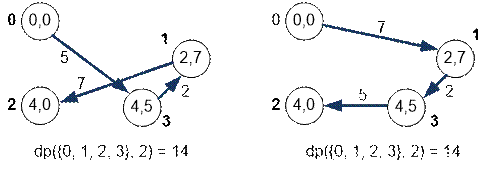
Рассмотрим
гамильтоновы пути по вершинам {0, 2, 3}, если путь завершается в вершине 2 (слева) или в вершине 3 (справа).
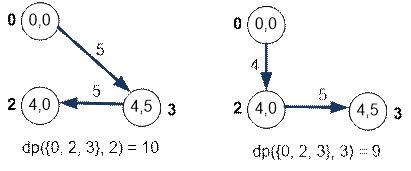
Найдем минимальную
длину гамильтонова пути по первым четырем вершинам, который завершается в
вершине 1:
dp({0, 1, 2, 3},
1) = min(dp({0, 2, 3}, 2) +
m[2][1], dp({0, 2, 3}, 3) + m[3][1]) =
min(10 + 7, 9 + 2) = min(14, 11) = 11
Минимум
достигается на слагаемом dp({0, 2, 3}, 3) + m[3][1], следовательно наилучшим путем будет
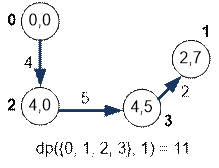
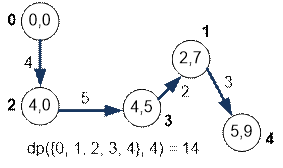
Найдем
минимальную длину гамильтонова пути по первым пяти вершинам, который
завершается в вершине 4:
dp({0, 1, 2, 3, 4}, 4) = min(dp({0, 1, 2, 3}, 1) + m[1][4],
dp({0, 1, 2, 3}, 2) + m[2][4],
dp({0, 1, 2, 3}, 3) + m[3][4])
=
min(11 + 3, 14 + 9, 13 + 4) =
min(14, 23, 17) = 14
Реализация алгоритма
Определим
переменную INF, условно равную бесконечности, максимально возможное число вершин
в графе MAX и массив dp, в котором будем хранить динамически пересчитываемые
значения dp(S, i). Каждое подмножество S будем хранить в виде числа, в
котором i - ый бит равен 1, если вершина с номером i в нем
присутствует, и нулю иначе. Например, при n = 5 подмножество {1, 4, 5}
кодируется числом 110012 = 25.
#define INF 100000000
#define MAX 16
int dp[1<<MAX][MAX+1];
Карту острова
храним в символьном массиве mas, координаты орехов и начального положения Лари
– в массивах x и y, матрицу смежности графа – в массиве m.
int x[21], y[21], m[21][21];
char mas[21][21];
Функция solve
вычисляет значение dp(S, last), где множество S кодируется целым числом mask.
При этом S \ {last} равно mask ^ (1<< last). Далее перебираем все i, i
Î S \ {last} и ищем минимальное значение res
среди dp(S \ {last}, i) + m[i][last]. Переменная res
указывает на ячейку dp[mask][last], так что с изменением res
изменяется и само значение dp[mask][last].
int solve(int
mask, int last)
{
int &res
= dp[mask][last];
if(res ==
INF)
{
mask
^= (1 << last);
for(int i = 1; i < nuts; ++i)
if(mask
& (1 << i)) res = min(res,solve(mask,i) + m[i][last]);
}
return res;
}
Основная часть
программы. Читаем данные острова в массив mas, заносим координаты орехов в
массивы x и y. Начальное местоположение Лари сохраняем в (x[0], y[0]).
while(scanf("%d
%d\n",&xx,&yy) == 2)
{
for(i = 0; i
< xx; i++) gets(mas[i]);
nuts = 1;
for(i = 0; i
< xx; i++)
for(j = 0; j
< yy; j++)
if
(mas[i][j] == 'L')
{
x[0] = i; y[0] = j;
} else
if
(mas[i][j] == '#')
{
x[nuts] = i; y[nuts++] = j;
}
Число вершин
графа, равное количеству орехов на острове плюс один (начальное состояние Лари),
хранится в переменной nuts. Если орехов на острове нет, то выводим 0.
if (nuts ==
1)
{
printf("0\n");
continue;
}
Строим матрицу
смежности графа m. Вычисляем длины ребер.
memset(m,0x3F,sizeof(m));
for(i = 0; i
< nuts - 1; i++)
for(j = i +
1; j < nuts; j++)
m[i][j] = m[j][i] = max(abs(x[i] - x[j]),
abs(y[i] - y[j]));
Изначально значения
dp(S, i) неизвестны, положим их равными плюс бесконечности. Множеству
{0} соответствует маска 1, положим dp({0}, 0) = 0 (минимальный путь из нулевой
вершины в нее же без посещения других вершин равен нулю). В переменной total
храним искомую минимальную длину цикла.
memset(dp,0x3F,sizeof(dp));
dp[1][0] = 0; total = INF;
Положим dp({0, i}, i) = m[0][i] (вершина
0 – местоположение Лари).
for(i = 1; i < nuts; i++) dp[1 | (1
<< i)][i] = m[0][i];
Вычисляем
гамильтонов цикл минимальной длины. Значение 2nuts – 1
соответствует множеству {0, 1, 2, ..., nuts – 1}. Вычисляем минимум среди всех значений dp({0, 1, 2, ..., nuts – 1}, i) + m[i][0], 1 £ i < nuts.
for(i = 1; i
< nuts; i++)
total = min(total, solve((1 << nuts)
- 1,i) + m[i][0]);
Выводим искомую
минимальную длину цикла.
printf("%d\n",total);
}