2303. Список телефонных номеров
По заданному списку телефонных
номеров необходимо определить, является ли он совместимым, то есть не содержит
ли он таких пар номеров, где один номер является префиксом другого.
Рассмотрим пример телефонного
каталога:
·
Экстренная
служба: 911
·
Алиса:
97 625 999
·
Боб:
91 12 54 26
В этом случае позвонить Бобу
невозможно, потому что при наборе его номера после первых трёх цифр вы сразу
попадёте в экстренную службу. Следовательно, данный список несовместим.
Вход. Первая строка содержит целое число t (1 ≤ t ≤ 40) – количество тестов.
Каждый тест начинается со строки,
содержащей целое число n (1 ≤ n ≤ 106) –
количество телефонных
номеров.
Далее следуют n строк, каждая
из которых содержит один телефонный номер, состоящий не более чем из 10 цифр.
Выход. Для каждого теста выведите строку “YES”, если список телефонных номеров
совместим, и “NO” в
противном случае.
|
Пример
входа |
Пример
выхода |
|
2 3 911 97625999 91125426 5 113 12340 123440 12345 98346 |
NO YES |
РЕШЕНИЕ
структуры данных – бор
Анализ алгоритма
Реализуем
структуру данных – бор (префиксное дерево) и занесём в неё все телефонные
номера. Если в вершине бора заканчивается слово, пометим её флагом leaf
= 1.
При добавлении
очередного номера s в бор проверим два условия:
·
не является ли s префиксом какого-либо уже
добавленного номера;
·
не существует ли номера, который является префиксом самого
s.
Также отдельно
проверим, нет ли в списке полностью совпадающих телефонных номеров.
Если ни одно из
этих условий не выполняется, то входной набор телефонных номеров считается
совместимым.
Пример
Пусть в бор уже добавлен
номер телефона 911. Если далее встретится номер 9112, то при его вставке мы
дойдём до вершины 3, которая уже помечена как конечная. Это означает, что для
номера 9112 уже существует другой номер, являющийся его префиксом.
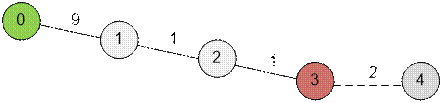
Рассмотрим другой случай: пусть следующим номером будет
91. После его вставки мы окажемся в вершине 2. Однако из этой вершины
существует переход в другие вершины (например, в вершину 3). Это значит, что
номер 91 является префиксом номера, который уже был ранее добавлен в бор.
Реализация алгоритма
Пусть item – структура, описывающая вершину бора. Алфавит бора состоит из цифр от 0 до 9. Структура
содержит конструктор, который при создании вершины инициализирует все указатели
значением -1.
struct item
{
int next[10];
int leaf;
item()
{
for (int i = 0; i < 10; i++) next[i] = -1;
leaf = 0;
}
};
Бор хранится в
массиве trie.
vector<item> trie;
Функция Insert
вставляет в бор телефонный номер, заданный строкой s. Если во время
вставки обнаруживается несовместимость номеров (например, один номер является
префиксом другого), функция возвращает false. В противном случае
возвращает true.
bool Insert(string& s)
{
int v = 0;
Проходим по всем символам строки
s, вставляя её в бор.
for (char ch : s)
{
Рассматриваем текущий символ ch строки s,
которому соответствует цифра d.
int d = ch - '0';
Если из теущей вершины trie[v] нет перехода по символу d, создаем
новую вершину бора.
if (trie[v].next[d] == -1)
{
trie[v].next[d] = trie.size();
trie.push_back(item());
}
Выполняем
переход по символу d к следующей вершине.
v = trie[v].next[d];
Если вершина v является концом какого-то другого слова
(leaf = 1), то новое вставляемое
слово s имеет в качестве префикса уже существующее слово. А это недопустимо по условию задачи. Номера не должны быть
префиксами друг друга. Возвращаем false.
if (trie[v].leaf) return false;
}
Обработка строки s завершена.
Если из текущей вершины trie[v] можно перейти хотя бы в одну другую
вершину (то есть существует индекс i, для которого trie[v].next[i]
≠ -1), значит, уже было добавлено слово, для которого s является
префиксом.
for (int i = 0; i < 10; i++)
if (trie[v].next[i] != -1) return false;
Отмечаем завершение слова s в текущей вершине trie[v],
устанавливая соответствующий флаг.
trie[v].leaf = true;
return true;
}
Основная часть
программы. Читаем входные данные.
cin >> tests;
while (tests--)
{
cin >> n;
Очищаем бор и устанавливаем его размер равным единице – изначально в боре
содержится только одна вершина (корень). Поскольку все телефонные номера
изначально считаются совместимыми, переменной flag присваивается
значение 0.
trie.clear(); trie.resize(1);
flag = 0;
Читаем все
телефонные номера и поочерёдно заносим их в бор. Даже если на каком-то этапе
была обнаружена несовместимость номеров, необходимо продолжить чтение
оставшихся номеров до конца, так как входные данные могут содержать несколько
тестов.
for (i = 0; i < n; i++)
{
cin >> s;
if (!Insert(s)) flag = 1;
}
После обработки всех номеров выводим результат в
зависимости от значения переменной flag.
if (flag) cout << "NO" << endl;
else cout << "YES" << endl;
}
Реализация при помощи класса
Объявим класс Node,
представляющий вершину бора.
Поле leaf принимает
значение 1, если текущая вершина соответствует окончанию какого-либо слова.
Поле out принимает
значение 1, если из текущей вершины имеются исходящие рёбра, то есть слово,
заканчивающееся в этой вершине, является префиксом некоторого другого слова.
class Node
{
public:
int next[10];
int out,
leaf;
Node()
{
for(int i = 0; i < 10; i++) next[i] = -1;
out = leaf = 0;
}
};
Объявим класс Trie. Все вершины бора будут храниться в
векторе trie.
class Trie
{
public:
vector<Node> trie;
Trie()
{
trie.clear();
trie.resize(1);
}
Вставка слова s в бор.
void Insert(char *s)
{
int v = 0;
for (int i = 0; i < strlen(s); ++i)
{
char c =
s[i]-'0';
if
(trie[v].next[c] == -1)
{
trie[v].next[c] = trie.size();
trie[v].out++;
trie.push_back(Node());
}
v = trie[v].next[c];
}
trie[v].leaf ++;
}
Функция CheckTrie проверяет,
является ли набор слов в боре совместимым. То есть никакая вершина не должна
быть окончанием более одного слова (trie[i].leaf ≤ 1). А
также следует проверить, что никакое слово, оканчивающееся в вершине i,
не является префиксом никакого другого
слова.
int
CheckTrie(void)
{
for(int i = 0; i < trie.size(); i++)
if
((trie[i].leaf > 1) || ((trie[i].leaf == 1) && (trie[i].out)))
return
1;
return 0;
}
};
Создадим указатель на бор.
Trie *t;
Основная часть
программы. Читаем входные данные.
scanf("%d",&tests);
while(tests--)
{
scanf("%d\n",&n);
Для каждого следующего теста создаем
новый бор.
t = new
Trie();
Читаем входные номера телефонов,
заносим их в бор.
for(int i = 0; i < n; i++)
{
gets(number);
t->Insert(number);
}
Проверяем набор телефонных номеров на
совместимость.
if
(t->CheckTrie()) printf("NO\n");
else printf("YES\n");
}
Реализация без STL, бор моделируем
массивом
Пусть node – структура
вершины бора. Она содержит:
·
10 указателей next[i] на цифры от 0 до 9.
·
Переменная leaf содержит количество слов, которые заканчиваются в вершине.
·
Переменная out содержит количество указателей, исходящих из вершины.
Бор содержит до
106 слов, каждое из
которых состоит из не более 10 символов. Следовательно размер бора не более MAX = 106 * 10 = 107.
#define MAX 10000001
struct node
{
int next[10];
int out, leaf;
};
Объявим бор tries как массив структур node. Размер бора
храним в переменной TrieSize.
node tries[MAX];
int TrieSize;
Функция init добавляет вершину в бор. В переменные leaf и out заносим 0. Указатели next[i] инициализируем
значением -1.
int init(void)
{
tries[TrieSize].leaf = 0;
tries[TrieSize].out = 0;
for(int i = 0; i < 10; i++)
tries[TrieSize].next[i] = -1;
return
TrieSize++;
}
Функция Insert вставляет в бор номера телефона, заданный в строке s.
void Insert(string &s)
{
Корень бора находится в вершине v =
0.
int v = 0;
Проходим по всем символам слова s, вставляя его в бор.
for (int i = 0; i < s.size(); i++)
{
Извлекаем следующий символ c из строки s.
char c = s[i] - '0';
Если из теущей вершины trie[v] нет перехода по символу c, то создаем новую вершину бора.
if (trie[v].next[c] == -1)
trie[v].next[c] = init();
trie[v].out++;
Совершаем переход по символу c.
v = trie[v].next[c];
}
В вершине v завершается обработка слова s.
trie[v].leaf++;
}
Функция CheckTrie проверяет,
является ли набор слов в боре совместимым. То есть никакая вершина не должна
быть окончанием более одного слова (trie[i].leaf ≤ 1). А
также следует проверить, что никакое слово, оканчивающееся в вершине i,
не является префиксом никакого другого
слова.
int CheckTrie(void)
{
for (int i = 0; i < TrieSize; i++)
if ((trie[i].leaf > 1)
|| ((trie[i].leaf == 1) && (trie[i].out)))
return 0;
return 1;
}
Основная часть
программы. Читаем входные данные. Обрабатываем test тестов.
cin >> test;
while (test--)
{
cin >> n;
Инициализируем бор. Устанавливаем его длину равной единице:
это единственная вершина – корень бора.
TrieSize = 0;
init();
Читаем телефонные номера. Заносим их
в бор. Даже если на каком-то этапе обнаружена несовместимость номеров – все
равно следует дочитать номера до конца, так как входные данные содержат
несколько тестов.
for(i = 0; i
< n; i++)
{
cin >> s;
Insert(s);
}
Проверяем набор телефонных номеров на
совместимость и выводим ответ.
if (CheckTrie()) cout << "YES" << endl;
else cout << "NO" << endl;
}