2304. Ужасные запросы
Мир
становится все более злым и поэтому становится все сложнее попасть в Лигу Зла.
Поскольку легендарная Плохая Лошадь ушла в отставку, теперь Вам следует
правильно ответить на злые вопросы Доктора Ужасного, который имеет докторскую степень
в ужасности (это не область компьютерных наук). У вас имеется массив из n элементов, изначально равных 0. Далее
Вам заданы c следующих команд:
·
0 p q v – следует прибавить значение v ко всем элементам массива с индексами
от p до q включительно.
·
1 p q –
вывести строку, содержащую единственное число – сумму всех элементов массива
между p и q включительно.
Вход. Первая строка содержит количество
тестов t. Каждый тест начинается со
значений n (n ≤ 105) и c (c ≤ 105). Далее следуют c команд в выше описанном формате. Известно,
что 1 ≤ p, q ≤ n и 1 ≤ v ≤ 107.
Выход. Вывести ответы на запросы.
|
Пример
входа |
Пример
выхода |
|
1 8 6 0 2 4 26 0 4 8 80 0 4 5 20 1 8 8 0 5 7 14 1 4 8 |
80 508 |
РЕШЕНИЕ
структуры
данных – дерево отрезков
Анализ алгоритма
Для решения
задачи следует реализовать дерево отрезков, поддерживающее групповую
модификацию – прибавление и суммирование.
В каждом узле
дерева будут поддерживаться значения двух переменных: суммы на отрезке summa и некоторого дополнительного
значения add, которое следует
прибавить ко всем элементам отрезка. Протолкнуть
значение add по дереву на один
уровень ниже означает прибавить его к значению summa левого и правого поддерева, умноженного на длину
соответствующего отрезка, а также к значению add левого и правого поддерева, тем самым рекурсивно обеспечив
проталкивание значения add до листьев
дерева.

Операцию
проталкивания следует производить не только при выполнении операции прибавления
на отрезке, но и при вычислении сумм.
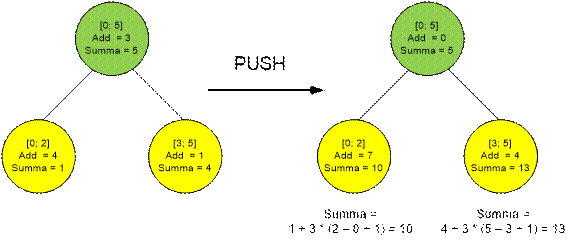
Пример
Пусть некоторая
вершина соответствует отрезку [0; 5]. Ее сыновьями являются отрезки [0; 2] и
[3; 5]. Рассмотрим операцию проталкивания на примере.
Реализация
алгоритма
Дерево отрезков храним в виде массива t
структур node длины MAX, где MAX
– максимальное количество элементов, которое может храниться в отрезке.
#define MAX 100000
struct
node
{
long long
summa, add;
} SegTree[4*MAX];
Функция Push производит проталкивание
значения add вершины v в сыновья. Если add ≠ 0, то его
следует протолкнуть на один уровень вниз. После проталкивания значение add в
вершине v ставим равным 0.
void Push(int v, int lpos, int mid, int rpos)
{
if (SegTree[v].add == 0) return;
SegTree[2*v].add +=
SegTree[v].add;
SegTree[2*v].summa += (mid - lpos + 1) * SegTree[v].add;
SegTree[2*v+1].add +=
SegTree[v].add;
SegTree[2*v+1].summa += (rpos - mid) * SegTree[v].add;
SegTree[v].add = 0;
}
Функция AddValue прибавляет ко
всем элементам отрезка [left; right] значение val. Вершине v соответствует
отрезок [lpos; rpos].
void AddValue(int v, int lpos, int rpos, int left, int right, int val)
{
if (left > right) return;
Если [left; right] соответствует отрезку, который
хранится в вершине дерева [lpos; rpos], то прибавляем
в текущей вершине дерева переменным add и summa соответствующие значения.
if ((lpos == left) && (rpos == right))
{
SegTree[v].add += val;
SegTree[v].summa += 1LL *
(right - left + 1) * val;
return;
}
Находим середину
отрезка mid = (lpos + rpos) / 2.
int mid = (lpos + rpos) / 2;
Проведем
проталкивание, если add не равно
нулю.
Push(v, lpos, mid, rpos);
Рекурсивно обрабатываем левого и правого сына текущей вершины
дерева отрезков.
AddValue(2*v, lpos, mid, left, min(mid, right), val);
AddValue(2*v+1, mid+1, rpos, max(left, mid + 1), right, val);
Пересчитываем значение суммы в вершине v через значения сумм ее детей.
SegTree[v].summa = SegTree[2*v].summa + SegTree[2*v+1].summa;
}
Функция Summa
возвращает значение суммы на отрезке [left; right]. Вершине v соответствует отрезок
[lpos; rpos].
long long Summa(int v, int lpos, int rpos, int left, int right)
{
if (left > right) return 0;
Если [left; right] совпадает с отрезком [lpos; rpos], который хранится в вершине v дерева, то возвращаем находящееся в ней значение суммы.
if ((lpos == left) && (rpos == right))
return SegTree[v].summa;
Находим середину
отрезка mid = (lpos + rpos) / 2.
int mid = (lpos + rpos) / 2;
Проведем
проталкивание, если add не равно
нулю.
Push(v, lpos, mid, rpos);
Разбиваем
отрезок [lpos; rpos] на [lpos; mid] и [mid + 1; right]. Запускаем рекурсивно вычисление сумм на подотрезках.
Складываем полученные суммы.
return Summa(2*v, lpos, mid, left, min(mid, right)) +
Summa(2*v+1, mid+1, rpos, max(left, mid+1), right);
}
Основная часть программы.
scanf("%d",&tests);
while(tests--)
{
Для каждого
теста читаем входные данные и строим дерево отрезков. Поскольку изначально все
элементы дерева отрезков равны нулю (значение add каждой вершины можно проинициализировать нулем, так как по
условию задачи в командах прибавляемое значение всегда натурально и не может
равняться нулю), то в качестве инициализации достаточно просто заполнить нулями
массив SegTree. Функцию построения дерева отрезков можно не
использовать.
scanf("%d %d",&n,&c);
memset(SegTree,0,sizeof(SegTree));
Последовательно обрабатываем c команд.
for(i = 0; i < c; i++)
{
scanf("%d %d %d",&command,&p,&q);
if (command == 0)
{
scanf("%d",&v);
AddValue(1,1,n,p,q,v);
} else printf("%lld\n",Summa(1,1,n,p,q));
}
}
Реализация с помощью
класса
#include <cstdio>
#include <vector>
#include <algorithm>
using namespace std;
class SegmentTree
{
public:
const static int NONE_ASSIGN = 0;
vector<long long> Summa, Add;
int len;
SegmentTree(int n)
{
len = n;
Summa.resize(4*n);
Add.resize(4*n);
BuildZeroTree(1, 1, len);
}
void BuildZeroTree(int v, int lpos, int rpos)
{
if (lpos == rpos)
{
Summa[v] = 0;
Add[v] = NONE_ASSIGN;
}
else
{
int mid = (lpos + rpos) / 2;
BuildZeroTree(2*v, lpos, mid);
BuildZeroTree(2*v+1, mid + 1, rpos);
Summa[v] = Summa[2*v] + Summa[2*v+1];
Add[v] = NONE_ASSIGN;
}
}
void Push(int v, int lpos, int mid, int rpos)
{
if (Add[v] == NONE_ASSIGN) return;
Add[2*v] += Add[v];
Summa[2*v] += (mid - lpos + 1) * Add[v];
Add[2*v+1] += Add[v];
Summa[2*v+1] += (rpos - mid) * Add[v];
Add[v] = NONE_ASSIGN;
}
void AddValue(int left, int right, int val)
{
AddValue(1, 1, len, left, right, val);
}
void AddValue(int v, int lpos, int rpos,
int left, int right, int val)
{
if (left > right) return;
if ((lpos == left) && (rpos == right))
{
Add[v] += val;
Summa[v] += (long long)(right - left + 1) * val;
return;
}
int mid = (lpos + rpos) / 2;
Push(v, lpos, mid, rpos);
AddValue(2*v, lpos, mid, left, min(mid, right), val);
AddValue(2*v+1, mid+1, rpos, max(left, mid+1), right, val);
Summa[v] = Summa[2*v] + Summa[2*v+1];
}
long long Sum(int left, int right)
{
return Sum(1, 1, len, left, right);
}
long long Sum(int v, int lpos, int rpos, int left, int right)
{
if (left > right) return 0;
if ((lpos == left) && (rpos == right)) return Summa[v];
int mid = (lpos + rpos) / 2;
Push(v, lpos, mid, rpos);
return Sum(2*v, lpos, mid, left, min(mid, right)) +
Sum(2*v+1, mid+1, rpos, max(left, mid+1), right);
}
};
int i, n, c, tests, command;
int L, R, p, q, v;
int main(void)
{
scanf("%d", &tests);
while (tests--)
{
scanf("%d %d", &n, &c);
SegmentTree s(n);
for (i = 0; i < c; i++)
{
scanf("%d %d %d", &command, &p, &q);
if (command == 0)
{
scanf("%d", &v);
s.AddValue(p, q, v);
}
else printf("%lld\n", s.Sum(p, q));
}
}
return 0;
}