2317. LCA offline (Easy)
Изначально имеется дерево,
состоящее только из корня (вершина с номером 1). Требуется научиться отвечать
на следующие запросы:
·
ADD a b – подвесить
вершину b за вершину a (гарантируется, что вершина a уже существует).
·
GET a b – вернуть
LCA вершин a и b.
Вершины имеют номера от 1 до n. В каждый момент времени у нас имеется
одно дерево.
Вход. В первой строке содержится
количество запросов k. Следующие k строк содержат сами запросы.
Гарантируется, что число запросов каждого из типов не превосходит 1000.
Выход. Для каждого запроса типа GET выведите в отдельную строку
одно целое число – ответ на соответствующий запрос.
|
Пример входа |
Пример выхода |
|
9 ADD 1 2 ADD 1 3 ADD 2 4 GET 1 3 GET 2 3 GET 3 4 ADD 2 5 GET 4 5 GET 5 5 |
1 1 1 2 5 |
РЕШЕНИЕ
структуры данных – Least Common Ancestor
Анализ алгоритма
Сведем задачу к
RMQ за время O(n). Препроцессинг RMQ
требует O(nlogn) по времени и памяти. Выполнение запроса GET будет производиться
за O(1).
Задача также
может быть решена методом двоичного подъема.
Пример
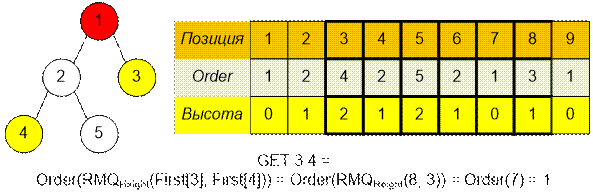
Отобразим дерево,
построенное в примере. Выполним на нем несколько запросов.
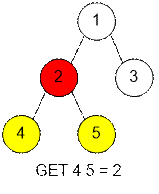
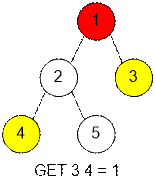
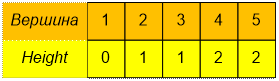
Содержимое массива Height – высоты вершин:
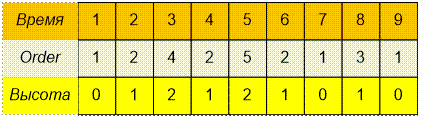
Массив порядка обхода вершин
Order с соответствующими им высотами:
Содержимое массива First (First[i] содержит наименьший индекс, в котором в массиве Order стоит вершина i):

Выполним на
дереве несколько запросов.

Реализация
алгоритма
Таблицу
RMQ будем строить в массиве mas. MAX – наибольшее возможное количество вершин в
дереве.
#define MAX 1010
#define LOGMAX 10
int mas[2*MAX][LOGMAX+1];
Дерево храним как граф в списке смежности g. Массивы Order, Height и First
используются для сведения задачи LCA к RMQ. Все поступающие запросы поместим в
массив пар Query.
vector<vector<int> > g;
vector<int> Order, used, Height, First;
vector<pair<int,int> >
Query;
int *hRMQ;
По массиву a размера size
строим массив mas, для которого
mas[i][j] = arg min(ai, ai+1, …, ai+2^j-1)
void
BuildRMQ(int *a, int
size)
{
int i, j;
for (i = 0; i
<= size; i++) mas[i][0] = i;
for (j = 1; 1
<< j <= size; j++)
for (i = 1;
i + (1 << j) - 1 <= size; i++)
if
(a[mas[i][j - 1]] < a[mas[i + (1 << (j - 1))][j - 1]])
mas[i][j] = mas[i][j - 1];
else
mas[i][j] = mas[i + (1 << (j - 1))][j - 1];
}
Функция RMQ возвращает минимум на
отрезке (ai, ai+1, …, aj) за O(1).
int
RMQ(int i, int
j)
{
if (i > j)
swap(i,j);
int k = 0;
while ((1
<< (k + 1)) <= j - i + 1) k++;
int res =
mas[i][k];
if
(hRMQ[mas[j - (1<<k) + 1][k]] < hRMQ[res])
res = mas[j - (1<<k) + 1][k];
return res;
}
Обход дерева в глубину. Порядок обхода вершин дерева (с фиксированием времени захода в вершину и возвращения в нее) сохраняем в массиве Order, их высоты – в массиве Height. Вызов dfs(v, h)
означает, что стартует поиск в глубину из вершины v, имеющей высоту h.
void
dfs(int v, int
h = 0)
{
used[v] = 1;
Order.push_back(v);
Height[v] = h;
for(int i = 0; i < g[v].size(); i++)
{
int to =
g[v][i];
if
(!used[to])
{
dfs(to, h + 1);
Order.push_back(v);
}
}
}
Препроцессинг LCA. Запускаем обход дерева в глубину.
Построение вспомогательных массивов. Выполняем препроцессинг RMQ по массиву
hRMQ, который содержит высоты последовательности вершин.
void
Init_LCA(void)
{
Order.push_back(0);
used.assign(MAX,0); Height.assign(MAX,0);
First.assign(MAX,0);
dfs(1);
First[i]
содержит момент времени, в который обход в глубину впервые заходит в вершину i.
for(int i = 1; i < Order.size(); i++)
if
(!First[Order[i]]) First[Order[i]] = i;
hRMQ = new int[Order.size()];
hRMQ[0] = 0;
for(int i = 1; i < Order.size(); i++)
hRMQ[i] = Height[Order[i]];
BuildRMQ(hRMQ, Order.size());
}
Функция LCA возвращает вершину
дерева, являющуюся LCA(i, j).
int
LCA(int i, int
j)
{
int index =
RMQ(First[i],First[j]);
return
Order[index];
}
Основная часть программы. Читаем входное дерево, заполняем
структуру g. Запросы собираем в массив пар Query.
scanf("%d\n",&k);
g.assign(MAX,vector<int>());
for(i
= 0; i < k; i++)
{
scanf("%s %d
%d\n",op, &a,&b);
if (op[0] == 'A') {g[a].push_back(b); g[b].push_back(a);}
else
Query.push_back(make_pair(a,b));
}
Сводим задачу LCA к RMQ.
Init_LCA();
Последовательно обрабатываем
запросы. Выводим ответ на каждый из них за O(1).
for(i
= 0; i < Query.size(); i++)
printf("%d\n",LCA(Query[i].first,Query[i].second));
Удаляем из памяти динамический
массив.
delete[] hRMQ;
Реализация
алгоритма – двоичный подъем
#include <cstdio>
#include <vector>
using namespace std;
int n, l, a, b, i, res;
Дерево храним в списке смежности g. Объявим массивы d и f меток времени при
обходе дерева в глубину. Объявим вспомогательный массив предков up.
vector<vector<int> > g;
vector<int> d, f;
int time;
vector<vector<int> > up;
vector<pair<int, int> > Query;
char op[20];
Запускаем
обход в глубину из вершины v. Предком
v является вершина p. Корнем дерева пусть является вершина
с номером 1.
void dfs(int v, int p = 1)
{
int i, to;
d[v] = time++;
Непосредственным
предком вершины v является p.
up[v][0] = p;
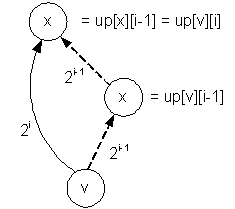
Для
нахождения 2i - го предка
вершины v сначала найдем 2i-1 - го предка
вершины v, равного x = up[v][i – 1]. После чего
найдем 2i-1 -
го предка вершины x, равного
up[v][i] = up[x][i – 1] = up[up[v][i
– 1] ][i – 1]
for (i = 1; i <=
l; i++)
up[v][i] = up[up[v][i - 1]][i - 1];
Продолжаем поиск в глубину.
Перебираем вершины to, куда можно
попасть из v.
for (i = 0; i <
g[v].size(); i++)
{
to = g[v][i];
Если to не является
предком v, то продолжаем поиск из вершины to.
if (to != p) dfs(to, v);
}
f[v] = time++;
}
Функция Parent возвращает 1, если
a является предком b.
int Parent(int a, int b)
{
return (d[a] <= d[b]) && (f[a] >= f[b]);
}
Функция
LCA
возвращает наименьшего общего предка вершин a
и b.
int LCA(int a, int b)
{
if (Parent(a, b)) return a;
if (Parent(b, a)) return b;
for (int i = l; i >=
0; i--)
if (!Parent(up[a][i], b)) a = up[a][i];
return up[a][0];
}
Основная часть программы. Читаем входные данные.
scanf("%d", &n);
g.resize(n + 1);
for (i = 0; i < n; i++)
{
scanf("%s %d
%d\n", op, &a, &b);
При запросе ADD добавляем ребро в дерево. При запросе GET сохраняем его
параметры в массиве Query.
if (op[0] == 'A') { g[a].push_back(b); g[b].push_back(a); }
else
Query.push_back(make_pair(a, b));
}
d.resize(n + 1); f.resize(n + 1); up.resize(n + 1);
Вычисляем l = ![]() . Инициализируем массив up.
. Инициализируем массив up.
l = 1;
while ((1 << l) <= n + 1)
l++;
for (i = 0; i <= n; i++) up[i].resize(l + 1);
Запускаем поиск в глубину из вершины 1.
dfs(1);
Вычисляем и выводим ответы на запросы типа GET.
for (i = 0; i < Query.size(); i++)
printf("%d\n", LCA(Query[i].first, Query[i].second));