2351. Dijkstra

The directed weighted graph is given. Find the shortest distance from one vertex to another.

Input. The first line contains three integers n, s and f (1 ≤ n ≤ 2000; 1 ≤ s, f ≤ n), where n is the number of graph vertices, s is the initial vertex, and f is the final vertex. Each of the next n lines contains n integers – the matrix of weights of the graph, where -1 means the lack of edge between the vertices, and any nonnegative integer – the weight of the existing edge. The main diagonal of the matrix contains zeroes.

Output. Print the shortest distance from s to f or -1 if the path does not exist.

Sample input	Sample output
3 1 2 0 -1 2 3 0 -1 -1 4 0	6

SOLUTION

graphs – Dijkstra algorithm

Algorithm analysis

The graph is given by the weight matrix. To solve the problem, it is necessary to implement Dijkstra’s algorithm.

Example

The graph shown in the sample has the form:

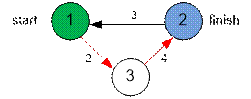
The shortest path from 1 to 2 equals to 2 + 4 = 6.

Algorithm realization

Implement Dijkstra’s algorithm using the weight matrix. Declare the global constants and arrays.

#define MAX 2001

#define INF 0x3F3F3F3F

int g[MAX][MAX], used[MAX], dist[MAX];

Function Relax relaxes the edge (i, j).

void Relax(int i, int j)

{

if (dist[i] + g[i][j] < dist[j])

dist[j] = dist[i] + g[i][j];

}

The main part of the program. Read the input data.

scanf("%d %d %d",&n,&s,&f);

Initialization of arrays.

memset(g,0x3F,sizeof(g));

memset(used,0,sizeof(used));

memset(dist,0x3F,sizeof(dist));

dist[s] = 0;

Read the weight matrix.

for(i = 1; i <= n; i++)

for(j = 1; j <= n; j++)

scanf("%d",&g[i][j]);

Start Dijkstra’s algorithm. The source is at the vertex s.

for(i = 1; i < n; i++)

{

min = INF; v = -1;

for(j = 1; j <= n; j++)

if (used[j] == 0 && dist[j] < min) {min = dist[j]; v = j;}

Graph can be disconnected. If v = -1, then the next vertex v is not found.

if (v < 0) break;

Relax the edges outgoing from the vertex v.

for(j = 1; j <= n; j++)

if (used[j] == 0 && g[v][j] != -1) Relax(v,j);

The shortest distance to the vertex v from the source s has already been calculated.

used[v] = 1;

}

Print the answer.

if (dist[f] == INF) printf("-1\n");

else printf("%d\n",dist[f]);

Java realization

import java.util.*;

public class Main

{

static final int INFINITY = 2000000000;

static int g[][], used[], dist[];

static void Relax(int i, int j)

{

if (dist[i] + g[i][j] < dist[j])

dist[j] = dist[i] + g[i][j];

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int s = con.nextInt();

int f = con.nextInt();

g = new int[n+1][n+1];

for (int[] row: g) Arrays.fill(row, INFINITY);

used = new int[n+1]; Arrays.fill(used, 0);

dist = new int[n+1]; Arrays.fill(dist, INFINITY);

dist[s] = 0;

for (int i = 1; i <= n; i++)

for (int j = 1; j <= n; j++)

g[i][j] = con.nextInt();

for (int i = 1; i < n; i++)

{

// find vertex w with minimum d[w] among not used vertices

int min = INFINITY, v = -1;

for (int j = 1; j <= n; j++)

if (used[j] == 0 && dist[j] < min) { min = dist[j]; v = j; }

// no more vertices to add

if (v < 0) break;

// relax all edges outgoing from v

// process edge v -> j

for (int j = 1; j <= n; j++)

if (used[j] == 0 && g[v][j] != -1) Relax(v, j);

// shortest distance to v is found

used[v] = 1;

}

if (dist[f] == INFINITY) System.out.println(-1);

else System.out.println(dist[f]);

con.close();

}

}