2379. Инверсии Джона

Джон недавно наткнулся на следующее определение инверсии. Инверсией в последовательности чисел s_k называется любая пара s_i, s_j такая что i < j и s_i > s_j.

Джон полагает, что инверсии являются идеальным инструментом для оценивания того, насколько хорошо последовательность чисел сортируется. Чем меньшее количество инверсий содержится в последовательности, тем лучше она сортируется. Например, если последовательность отсортирована в порядке возрастания, то она содержит ноль инверсий.

Петр дал Джону колоду из n карт. На каждой карте написано два числа – одно красного цвета, другое синего. Джон очень хочет проверить свои знания про инверсии, используя эту колоду.

Он кладет карты перед собой в произвольном порядке и вычисляет общее число хороших инверсий для последовательности чисел, расположенной перед ним. Джон считает инверсию хорошей, если она состоит из номеров одного и того же цвета. В нашем случае хорошая инверсия может быть сформирована либо двумя голубыми, либо двумя красными цифрами. Если количество хороших инверсий слишком велико по меркам Джона, то он перетасовывает карты и повторяет процесс.

Вам следует помочь Джону узнать минимальное возможное количество хороших инверсий следуя по описанному алгоритму.

Вход. Первая строка содержит количество карт n (1 ≤ n ≤ 100000) в колоде. Каждая из следующих n строк описывает одну карту. i-ая строка содержит два целых числа r_i и b_i (1 ≤ r_i, b_i ≤ 10⁹), записанные на i-ой карте красным и синим цветов соответственно.

Выход. Вывести минимальное возможное количество хороших инверсий.

Пример входа	Пример выхода
3 10 3 20 2 30 1	3

РЕШЕНИЕ

сортировка слиянием

Анализ алгоритма

Рассмотрим произвольное расположение карт. Джон вычисляет количество инверсий a, образованное красными числами, и количество инверсий b, образованное синими числами. Количество хороших инверсий Джона равно a + b. Эту сумму и хочет минимизировать Джон, переставляя карты.

Отсортируем карты, например, по красным числам. Далее подсчитаем количество инверсий по синим числам полученного ряда карт. Это значение и будет искомым количеством хороших инверсий. Действительно, сделав любую перестановку в таком порядке, мы только сможем увеличить количество инверсий.

То же самое количество инверсий мы получим, если отсортируем карты по синим числам, после чего подсчитаем количество инверсий по красным числам.

Пример

Рассмотрим расположение карт, отсортированных по красным числам.

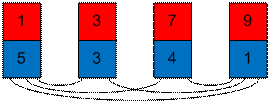
Синие числа образуют 5 инверсий. Начнем сортировать карты по синим числам. Возьмем карту с синим наименьшим числом (единицей) и поставим ее на новое место (на первое). До перестановки синяя 1 образовывала 3 инверсии. После перестановки карты синяя 1 не будет давать инверсий. Однако соответствующая ей красная 9 до перестановки не давала инверсий, а после перестановки будет образовывать 3 инверсии. То есть 3 синие инверсии превратятся в 3 красные.

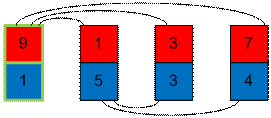
Теперь переставим карту со вторым наименьшим синим числом на свое место. Одна инверсия исчезнет у синих чисел, а одна добавится у красных.

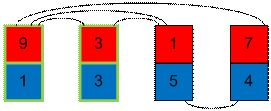
Остается поменять карты с синими 5 и 4. Одна инверсия у синих превратится в одну инверсию у красных.

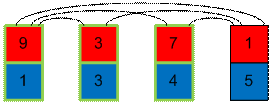
Реализация алгоритма

Число инверсий swaps будем подсчитывать в массиве m. Числа, записанные на картах, храним в массиве пар v.

#define MAX 100001

int m[MAX];

long long swaps;

vector<pair<int,int> > v;

Слияние a[bleft..bright] и a[cleft..cright] в a[bleft..cright]. Для этого используется дополнительный массив res. Сначала копируем a[bleft..bright] в res[0 .. len – 1], после чего сливаем res[0 .. len – 1] и a[cleft..cright].

void merge(int *a, int bleft, int bright, int cleft, int cright)

{

int i, len = bright - bleft + 1, resCur = 0;

int *res = new int[len];

memcpy(res,a + bleft,len*sizeof(int));

while((resCur < len) && (cleft <= cright))

{

if (res[resCur] <= a[cleft]) a[bleft++] = res[resCur++];

else a[bleft++] = a[cleft++], swaps += len - resCur;

}

while (resCur < len) a[bleft++] = res[resCur++];

delete[] res;

}

Сортировка слиянием массива a[left..right].

void mergeSort(int *a, int left, int right)

{

if (left >= right) return;

int middle = (left + right) / 2;

mergeSort(a,left,middle);

mergeSort(a,middle+1,right);

merge(a, left, middle, middle + 1, right);

}

Основная часть программы. Читаем числа на картах. Сортируем карты по возрастанию красных чисел.

scanf("%d",&n);

for(i = 0; i < n; i++)

{

scanf("%d %d",&a,&b);

v.push_back(make_pair(a,b));

}

sort(v.begin(),v.end());

Синие числа на картах занесем в массив m.

for(i = 0; i < n; i++)

m[i] = v[i].second;

Вычисляем и выводим количество инверсий в массиве m.

swaps = 0;

mergeSort(m, 0, n - 1);

printf("%lld\n",swaps);