2400. Треугольники
Миша любил
рисовать треугольники, но делал это необычным способом. Сначала он рисовал
произвольный треугольник, затем каждую его сторону делил на n равных
частей и через точки деления проводил прямые, параллельные сторонам
треугольника. В результате получалась сетка из одинаковых треугольников.
Помогите Мише
определить максимальное количество равных треугольников, которое может быть на
его финальном рисунке.

Вход. Одно целое число n
(0 < n < 2 * 109).
Выход. Выведите наибольшее
количество равных треугольников.
|
Пример
входа |
Пример
выхода |
|
2 |
4 |
РЕШЕНИЕ
комбинаторика
Анализ алгоритма
Рассмотрим треугольник,
каждая сторона которого разделена на n равных частей. Наибольшее
количество одинаковых фигур получится среди наименьших равных треугольников.
Посчитаем их число.
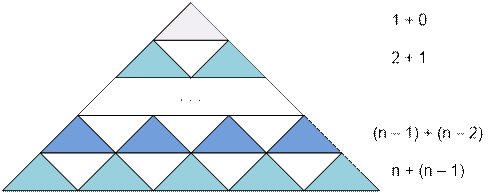
Разобьём
треугольник на n горизонтальных полос, пронумеровав их сверху вниз.
·
В последней, n-й (нижней) полосе находится n
треугольников с вершиной вверх и n – 1 треугольников с вершиной вниз.
·
В предпоследней, (n – 1)-й полосе – n – 1
треугольник с вершиной вверх и n – 2 треугольника с вершиной вниз.
Продолжая
рассуждение, получаем:
·
число треугольников с вершиной вверх равно n + (n
– 1) + (n – 2) + … + 2 + 1;
·
число треугольников с вершиной вниз равно (n – 1) + (n – 2) + … + 2 + 1.
Таким образом,
общее количество наименьших равных треугольников равно сумме этих двух величин:
2 * (n + (n
– 1) + (n – 2) + … + 2 + 1) – n = ![]() = n2
= n2
Пример
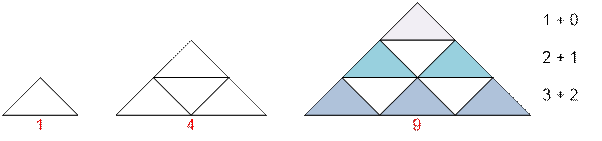
Для n = 1, 2 и 3 количество
равных треугольников составляет соответственно 1, 4 и 9. Например, при n
= 3 ответ равен (1 + 2 + 3) + (1 + 2) = 9.
Реализация алгоритма
Читаем входное значение
n.
scanf("%lld",&n);
Вычисляем и
выводим ответ.
res = n * n;
printf("%lld\n",res);
Java реализация
import java.util.*;
class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
long n = con.nextLong();
long res = n * n;
System.out.println(res);
con.close();
}
}
Python реализация
Читаем входное значение
n.
n = int(input())
Вычисляем и
выводим ответ.
res = n * n
print(res)