2400. Triangles
Misha loved
drawing triangles, but he did it in an unusual way. First, he drew an arbitrary
triangle. Then he divided each of its sides into n equal parts and drew lines through the division points, parallel to the
sides of the triangle. As a result, a grid of identical triangles was formed.
Help Misha
determine the maximum number of equal triangles that can appear in his final
drawing.

Input. One integer n (0 < n < 2 * 109).
Output. Print the maximum number
of equal triangles.
|
Sample
input |
Sample
output |
|
2 |
4 |
SOLUTION
combinatorics
Algorithm analysis
Consider a triangle whose
each side is divided into n equal parts. The largest number of identical
shapes will be among the smallest equal triangles. Let us count them.
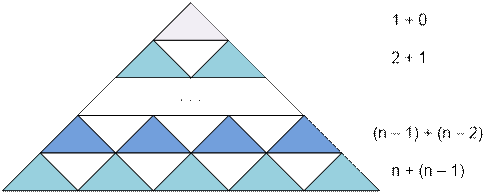
Let us divide the triangle
into n horizontal strips, numbered from top to bottom.
·
In the last, n-th (bottom) strip, there are n
triangles pointing upwards and n – 1 triangles pointing downwards.
·
In the penultimate, (n – 1)-th strip, there are n
– 1 triangles pointing upwards and n – 2 triangles pointing downwards.
Continuing this reasoning,
we obtain:
·
the number of triangles pointing upwards is n + (n – 1) + (n – 2) + … + 2 + 1;
·
the number of triangles pointing downwards is (n – 1) + (n – 2) + … + 2 + 1.
Thus, the total number of
the smallest equal triangles is the sum of these two quantities:
2 * (n + (n
– 1) + (n – 2) + … + 2 + 1) – n = ![]() = n2
= n2
Example
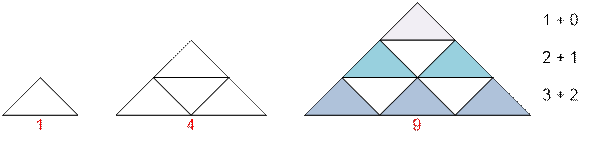
For n = 1, 2, and
3, the number of equal triangles is 1, 4, and 9, respectively. For example,
when n = 3, the answer is (1 + 2 + 3) + (1 + 2) = 9.
Algorithm implementation
Read the input value n.
scanf("%lld",&n);
Compute and print the answer.
res = n * n;
printf("%lld\n",res);
Java implementation
import java.util.*;
class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
long n = con.nextLong();
long res = n * n;
System.out.println(res);
con.close();
}
}
Python implementation
Read the input value n.
n = int(input())
Compute and print the
answer.
res = n * n
print(res)