2414. Сумма квадратов
Обозначим через
U(n) общее количество
последовательностей, состоящих только
из чисел 1 и 2, сумма членов которой,
равна n.
По заданному
значению n определите сумму квадратов
чисел U(i) для всех i = 1, …, n.
Результат выведите по модулю 109 + 9.
Вход. Одно натуральное число n (1 ≤ n ≤ 1018).
Выход. Выведите
значение ![]() mod (109 + 9).
mod (109 + 9).
|
Пример
входа |
Пример
выхода |
|
3 |
14 |
РЕШЕНИЕ
числа
Фибоначчи
Анализ алгоритма
Рассмотрим, что
собой представляет функция U(n). Очевидно,
что U(1) = 1 (одна последовательность из одной единицы), U(2) = 2 (две
последовательности 1, 1 и 2). Для всех натуральных n U(n) соответствует
рекуррентности Фибоначчи:
![]()

Например, для начальных
значений n можно получить следующие
последовательности:
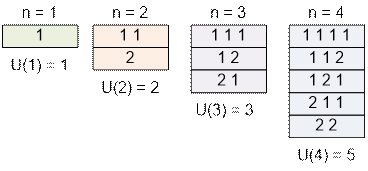
Числа Фибоначчи
имеют следующий вид:

В задаче
требуется найти сумму
U(1)2
+ U(2)2 + … + U(n)2
= F(2)2 + F(3)2 + … + F(n+1)2 = F(n+1)
* F(n+2) – 1
Осталось
реализовать вычисление чисел Фибоначчи F(n) за время O(log2n).
Сумма квадратов
чисел Фибоначчи имеет геометрическую интерпретацию. Составим прямоугольник из
квадратов с длинами сторон F(1), F(2), …, F(n) как показано на рисунке. Тогда площадь
прямоугольника равна F(n) * F(n + 1).
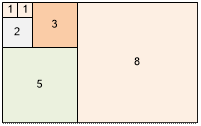
F(1)2
+ F(2)2 + F(3)2 + F(4)2 + F(5)2 + F(6)2 =
12 + 12 + 22
+ 32 + 52 + 82 = 8 * 13 = F(6) * F(7)
Таким образом
F(1)2
+ . . . + F(n)2 =
F(n) * F(n + 1)
Эту формулу
можно доказать при помощи метода математической индукции:
1. База
индукции: n = 1. F(1)2 = F(1) * F(2) или 12 =
1 * 1, что верно.
2. Шаг индукции.
F(1)2
+ . . . + F(n)2 +
F(n + 1)2 =
F(n) * F(n + 1) + F(n + 1)2 =
= F(n + 1) * (F(n) + F(n + 1)) = F(n + 1) * F(n + 2)
Пример
Для n = 3 имеем:
U(1)2
+ U(2)2 + U(3)2 =
F(2)2
+ F(3)2 + F(4)2 = F(4) * F(5) – 1 = 3 * 5 – 1 = 14
Реализация алгоритма
Объявим модуль
MOD, вычисления по которому будем производить.
#define MOD 1000000009
Реализуем вычисление чисел Фибоначчи через возведение матрицы
в степень.
class Matrix
{
public:
long long a, b, c, d;
Matrix(long long a = 1, long long b = 0,
long long c = 0, long long d = 1)
{
this->a = a; this->b = b;
this->c = c; this->d = d;
}
Matrix operator* (const Matrix &x)
{
Matrix res;
res.a =
(a * x.a + b * x.c) % MOD;
res.b =
(a * x.b + b * x.d) % MOD;
res.c =
(c * x.a + d * x.c) % MOD;
res.d =
(c * x.b + d * x.d) % MOD;
return res;
}
Matrix operator^ (long long n)
{
Matrix x(*this);
if (n == 0) return Matrix();
if (n & 1) return x * ((x * x) ^ (n / 2));
return (x * x) ^ (n / 2);
}
};
long long fib(long long n)
{
Matrix res(1, 1, 1, 0);
res = res ^ n;
return res.b;
}
Читаем входные данные, вычисляем и
выводим результирующее значение Fn+1
* Fn+2 – 1.
scanf("%lld",&n);
res = (fib(n+1)
* fib(n+2) + MOD - 1) % MOD;
printf("%lld\n",res);
Реализация алгоритма –
рекурсия с запоминанием
#include <cstdio>
#include <map>
#define MOD 1000000009
using namespace std;
map<long long, long long> fib;
long long f(long long n)
{
if (n == 0) return 1;
if (n == 1) return 1;
if (fib[n] != 0) return fib[n];
long long k = n / 2;
if (n % 2 == 0)
return fib[n] = (f(k - 1) * f(k - 1) + f(k) * f(k)) % MOD;
return fib[n] = (f(k) * (f(k - 1) + f(k + 1))) % MOD;
}
long long n, res;
int main(void)
{
scanf("%lld", &n);
res =
(f(n) * f(n + 1) + MOD - 1) % MOD;
printf("%lld\n", res);
return 0;
}