2479. Parentheses Balance

A string consisting of parentheses ( ) and square brackets [ ] is given. A bracket expression is considered correct if the following conditions are satisfied:

· The string is empty;

· If expressions A and B are correct, then their concatenation AB is also correct;

· If expression A is correct, then (A) and [A] are also correct.

Write a program that determines whether a given bracket expression is correct. The length of each string does not exceed 128 characters.

Input. The first line contains the number of test cases n. Each of the following n lines contains a bracket expression consisting of the characters (, ), [, and ].

Output. For each test case, print “Yes” if the expression is correct, and “No” otherwise, each on a separate line.

Sample input	Sample output
3 ([]) (([()]))) ([()[]()])()	Yes No Yes

SOLUTION

data structures - stack

Algorithm analysis

To solve this problem, we’ll use a character stack. As we iterate through the characters of the input string, perform the following actions:

· If the current character is an opening bracket (either round or square), we push it onto the stack.

· If the current character is a closing bracket, the top of the stack must contain the corresponding opening bracket. If this is not the case, or if the stack is empty, the bracket expression is considered incorrect.

After processing the entire string, the stack must be empty – this is the condition for the bracket sequence to be correct.

Example

Let’s examine how the algorithm works using the example string “( ( [ ] ) [ ] )”.

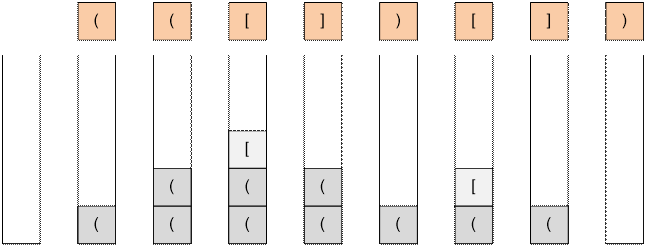
Algorithm implementation

Declare a stack s.

stack<char> s;

Read the number of test cases tests. Skip the ‘\n’ character.

cin >> tests;

getline(cin, str);

Process the tests test cases one by one.

while (tests--)

{

Read the input string str. It may be empty.

getline(cin, str);

The variable flag will be set to 1 if the input bracket expression is not correct. Initially, set flag = 0.

flag = 0;

Before processing each test case, clear the stack s.

while(!s.empty()) s.pop();

Iterate through the characters of the input string str.

for(i = 0; i < str.size(); i++)

{

Push an opening bracket onto the stack.

if ((st[i] == '(') || (str[i] == '[')) s.push(str[i]); else

If the current character str[i] is a closing bracket, pop a character from the top of the stack, which should be the corresponding opening bracket. If this is not the case, or if the stack is empty, set the variable flag to 1.

if (!s.empty() && ((str[i] == ')' && s.top() == '(') ||

(str[i] == ']' && s.top() == '['))) s.pop();

else flag = 1;

}

If flag = 0 and the stack is empty, then the bracket expression is correct.

if (flag == 0 && s.empty()) cout << "Yes\n"; else cout << "No\n";

}

Java implementation

import java.util.*;

public class Main

{

static char rev(char c)

{

return (c == ')') ? '(' : '[';

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int tests = con.nextInt();

String Line = con.nextLine();

while(tests-- > 0)

{

Line = con.nextLine();

Stack<Character> s = new Stack<Character>();

int Flag = 0;

for(int i = 0; i < Line.length(); i++)

{

if (Flag > 0) break;

if ((Line.charAt(i) == '(') || (Line.charAt(i) == '['))

s.push(Line.charAt(i));

if ((Line.charAt(i) == ')') || (Line.charAt(i) == ']'))

{

if (s.empty() || (s.peek() != rev(Line.charAt(i))))

Flag = 1;

else s.pop();

}

}

if (!s.empty()) Flag = 1;

if (Flag > 0) System.out.println("No");

else System.out.println("Yes");

}

}

}