2509. Почтовое отправление

Для подготовки заключительного этапа European Code Challenge организаторам понадобилось отправить на место проведения n предметов. Для каждого предмета известна его масса в граммах m_i.

Для пересылки было решено воспользоваться почтовой службой “Суперэкспресс”. Служба принимает к отправке бандероли, каждая из которых может содержать один или несколько предметов. Масса бандероли равна сумме масс всех вложенных в неё предметов.

Отправка бандероли стоит 1 евро за грамм, за исключением бандеролей, подпадающих под действие специального предложения: если бандероль весит ровно один килограмм, то стоимость её пересылки составляет p евро.

Организаторы European Code Challenge хотят отправить все предметы, потратив как можно меньшую сумму. Помогите им распределить предметы по бандеролям так, чтобы минимизировать общую стоимость пересылки.

Вход. Первая строка содержит два целых числа n и p (1 ≤ n ≤ 14; 1 ≤ p ≤ 1000) – количество предметов и стоимость пересылки бандероли по специальному предложению.

Вторая строка содержит n целых чисел m₁, m₂, ..., m_n (1 ≤ m_i ≤ 1000 для всех i от 1 до n).

Выход. Выведите одно число – минимальную суммарную стоимость пересылки всех предметов в евро.

Пример входа	Пример выхода
5 800 100 200 300 400 500	1300

РЕШЕНИЕ

динамическое программирование - маски подмножеств

Анализ алгоритма

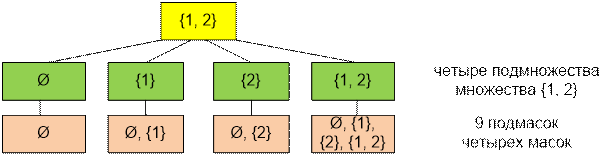
Введём понятие маски, описывающей подмножество пересылаемых предметов. Например, маска mask = 5 = 101₂ задаёт подмножество, включающее нулевой и второй предметы (предметы нумеруются с нуля).

Для каждого подмножества вычислим его суммарный вес, который определяет стоимость пересылки. Если этот вес ровно равен 1000 грамм, то, поскольку p ≤ 1000, всегда выгодно воспользоваться специальным предложением.

Пусть MinCost[mask] обозначает минимальную стоимость (в евро) пересылки подмножества предметов, заданного маской mask. Тогда для любой маски x, являющейся подмножеством mask, выполняется следующее соотношение:

MinCost[mask] =

Поскольку маска 2ⁿ – 1 соответствует всему множеству из n предметов, ответом задачи будет значение MinCost[2ⁿ – 1].

Теорема. Перебор всех масок и всех их подмасок выполняется за O(3ⁿ).

Доказательство 1. Рассмотрим i-ый бит. Для него возможны три варианта:

· он входит в маску mask и входит в подмаску sub;

· он входит в маску mask, но не входит в подмаску sub;

· он не входит ни в маску mask, ни в подмаску sub;

Всего битов n, значит общее число различных комбинаций равно 3ⁿ.

Доказательство 2. Пусть маска mask содержит k установленных битов. Тогда она имеет ровно 2^k подмасок. Количество масок длины n с ровно k установленными битами равно . Следовательно, общее число комбинаций равно

= (1 + 2)ⁿ = 3ⁿ

Реализация алгоритма

Массы предметов будем хранить в массиве m. В ячейке MinCost[mask] будем хранить минимальную стоимость пересылки подмножества предметов, задаваемого маской mask.

int m[15], MinCost[1 << 14];

Читаем входные данные.

scanf("%d %d",&n,&p);

for (i = 0; i < n; i++) scanf("%d",&m[i]);

В переменной mask перебираем все возможные маски от 0 до 2ⁿ – 1.

for (mask = 0; mask < (1 << n); mask++)

{

В переменную Cost занесем суммарный вес подмножества предметов, соответствующего маске mask. Для этого просмотрим двоичное представление числа mask: если на позиции i стоит 1, то добавим к Cost вес i-го предмета.

for (Cost = i = 0; i < n; i++)

if (mask & (1 << i)) Cost += m[i];

Если значение Cost строго равно 1000, то, поскольку по условию p ≤ 1000, присваиваем переменной Cost значение p.

if (Cost == 1000) Cost = p;

Занесём вычисленную стоимость пересылки в соответствующую ячейку массива MinCost.

MinCost[mask] = Cost;

}

Для каждой маски mask перебираем все подмножества x Ì mask (маска x является подмножеством mask тогда и только тогда, когда mask AND x равно x). Если из множества, соответствующего маске mask, вычесть множество, соответствующее x, то получится множество с маской mask XOR x.

Например, если mask = 1101₂, x = 1001₂, то mask XOR x = 100₂, что соответствует теоретико - множественной операции {1, 3, 4} \ {1, 4} = {3}.

for (mask = 0; mask < (1 << n); mask++)

for (x = 0; x < mask; x++)

Пересчитываем значение MinCost[mask] согласно рекуррентному соотношению, приведённому в анализе задачи.

if ((mask & x) == x)

MinCost[mask] = min(MinCost[mask],MinCost[mask^x] + MinCost[x]);

Выводим ответ, который находится в ячейке MinCost[2ⁿ – 1].

printf("%d\n",MinCost[(1 << n) - 1]);

Реализация с оценкой O(3ⁿ)

Объявим константу и массивы.

#define MAX 0xFFFFFFFF

unsigned int m[15], MinCost[1 << 14];

Для маски mask необходимо перебрать все её подмаски sub и найти минимум среди всех возможных значений

FindCost(sub) + FindCost(mask ^ sub)

Из-за симметрии этой суммы достаточно рассматривать только те подмаски sub, для которых выполняется условие sub ≥ mask ^ sub.

unsigned int FindCost(int mask)

{

if (MinCost[mask] != MAX) return MinCost[mask];

// sub перебирает все подмаски маски mask

for (int sub = (mask - 1) & mask;

sub >= mask ^ sub; sub = (sub - 1) & mask)

MinCost[mask] =

min(MinCost[mask], FindCost(sub) + FindCost(mask ^ sub));

return MinCost[mask];

}

Основная часть программы. Установим MinCost[mask] = -1 для всех масок, стоимость отправки соответствующего набора предметов для которых ещё не была вычислена.

memset(MinCost,0xFF,sizeof(MinCost));

Читаем входные данные.

scanf("%d %d",&n,&p);

for(i = 0; i < n; i++) scanf("%d",&m[i]);

Если стоимость некоторого подмножества предметов не превышает 1000 (именно не больше, а не меньше, так как возможен случай p = 1000), то специальное предложение для их отправки применить нельзя. Для таких подмножеств можно сразу вычислить MinCost[mask] как сумму стоимостей всех предметов. Если сумма стоимостей предметов ровно 1000, то присваиваем MinCost[mask] = p.

Таким образом мы предварительно заполняем известные минимальные стоимости для малых подмножеств. Это увеличивает эффективность работы программы.

for (mask = 0; mask < (1 << n); mask++)

{

for(Cost = i = 0; i < n; i++)

if (mask & (1 << i)) Cost += m[i];

if (Cost == 1000) Cost = p;

if (Cost <= 1000) MinCost[mask] = Cost;

}

Выводим ответ. Все множество предметов задается маской 2ⁿ – 1, двоичное представление которой состоит из n единиц.

printf("%u\n",FindCost((1 << n) - 1));