2523. Строки Фибоначчи
Последовательность
строк Фибоначчи определяется следующим образом:
·
s1 = “b”,
·
s2 = “a”,
·
sk = sk-1 + sk-2 для k > 2
Например, s3 = “ab”, s4 =
“aba”, s5 =
“abaab” и т.д.
Даны натуральные
числа n, m, l. Вывести подстроку строки sn, начинающуюся с позиции m и имеющую длину l.
Вход. Содержит одну строку, в которой находятся три разделённых
пробелом натуральных числа n, m и l (1 ≤ n ≤ 40; 1 ≤ m ≤ длина(Sn); 1 ≤ l ≤ 1000).
Выход. Вывести подстроку строки sn, начинающуюся с позиции m и имеющую длину l (длина выведенной подстроки может оказаться меньше,
если длина оставшейся части строки sn,
начинающейся с позиции m,
меньше l).
|
Пример
входа |
Пример
выхода |
|
5 3 10 |
aab |
РЕШЕНИЕ
рекурсия,
строки
Анализ алгоритма
Пусть fib(i) – i-ое
число Фибоначчи. Используя тот факт, что sn
= sn-1 + sn-2, будем искать
подстроку стоящую на позициях [m … m + l]
либо в sn-1,
либо в sn-2,
либо на их пресечении – то есть искомая подстрока является конкатенацией
суффикса sn-1 и
префикса sn-2.
Реализуем
функцию solve(n, Left,
Right), которая возвращает
подстроку Фибоначчи sn,
лежащую в позициях от Left до Right включительно.
Если n = 1 или n = 2, то возвращаем соответствующую строку, состоящую из одного
символа (s1 = b, s2 = a).
Поскольку sn является конкатенацией
строк sn-1 и
sn-2, то
попробуем установить, в какой из этих частей (sn-1 или sn-2)
лежит искомая подстрока. При этом длины sn-1
и sn-2 нам
известны (именно для этого мы посчитаем числа Фибоначчи в массиве fib).
·
Если Right
≤ fib(n – 1), то искомая
подстрока целиком лежит в sn-1.
Возвращаем solve(n – 1, Left, Right).
·
Если Left > fib(n – 1), то искомая подстрока полностью
лежит в sn-2.
При этом следует пересчитать индексы искомой подстроки, а именно вычесть из Left и Right длину sn-1.
Возвращаем solve(n – 2, Left – fib(n – 1), Right – fib(n – 1)).
·
Иначе искомая подстрока начинается в sn-1 и заканчивается в sn-2. Следует вернуть подстроку из sn-1 на позициях [Left … fib(n – 1)] и конкатенировать с подстрокой из sn-2 на позициях [1 … Right
– fib(n – 1)]. То есть возвращаем
solve(n – 1, Left, fib(n – 1)) + solve(n – 2, 1, Right – fib(n – 1)).
Пример
Пусть n = 7, m = 6,
l = 7.
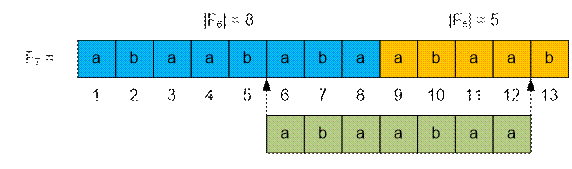
solve(7,
6, 12) = solve(7
– 1, 6, fib(6)) + solve(7 – 2, 1, 12 – fib(6)) =
= solve(6,
6, 8) + solve(5, 1, 4) = “aba” + “abaa” = “abaabaa”.
Реализация алгоритма
В массив fib занесем числа Фибоначчи:
fib[i] содержит длину si.
#define MAX 44
int fib[MAX] = {0, 1};
Реализуем функцию
solve.
string solve(int n, int Left, int Right)
{
if (n == 1) return "b";
if (n == 2) return "a";
if (Right
<= fib[n-1]) return solve(n-1,
Left, Right);
if (Left >
fib[n-1])
return solve(n-2, Left - fib[n-1], Right -
fib[n-1]);
return
solve(n-1, Left, fib[n-1]) + solve(n-2, 1, Right -
fib[n-1]);
}
Основная часть программы. Вычисляем
первые MAX чисел Фибоначчи.
for(int
i = 2; i < MAX; i++)
fib[i] = fib[i-1] + fib[i-2];
Читаем входные данные. Вычисляем и
выводим ответ.
scanf("%d %d %d",&n,&m,&l);
string res =
solve(n,m,m+l-1);
puts(res.c_str());
Java реализация
import java.util.*;
public class Main
{
public static int MAX =
44;
public static int fib[] = new int[44];
public static
String solve(int n, int Left, int Right)
{
if (n ==
1) return "b";
if (n ==
2) return "a";
if (Right
<= fib[n-1])
return solve(n-1, Left, Right);
if (Left >
fib[n-1])
return solve(n-2, Left - fib[n-1], Right - fib[n-1]);
return solve(n-1, Left, fib[n-1])
+
solve(n-2,
1, Right - fib[n-1]);
}
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
fib[1] =
1;
for(int i = 2;
i < MAX; i++)
fib[i] = fib[i-1] +
fib[i-2];
int n = con.nextInt();
int m = con.nextInt();
int l = con.nextInt();
String res = solve(n,m,m+l-1);
System.out.println(res);
con.close();
}
}