2523. Fibonacci strings

Fibonacci sequence of strings is defined as follows:

· s₁ = “b”,

· s₂ = “a”,

· s_k = s_k-1 + s_k-2 для k > 2

For example, s₃ = “ab”, s₄ = “aba”, s₅ = “abaab” and so on.

Given positive integers n, m, l. Print the substring s_n which starts at position m and have the length l.

Input. One line contains three positive integers n, m and l (1 ≤ n ≤ 40; 1 ≤ m ≤ length(S_n); 1 ≤ l ≤ 1000).

Output. Print the substring of s_n which starts at position m and have the length l (the length of the printed substring may be less if the length of the remainder of the string s_n, starting from position m, is less than l).

Sample input	Sample output
5 3 10	aab

SOLUTION

recursion, strings

Algorithm analysis

Let fib(i) be the i-th Fibonacci number. Using the fact that s_n = s_n-1 + s_n-2, we’ll look for a substring located at positions [m … m + l] either in s_n-1, or in s_n-2, or at their intersection – that is, the final substring is a concatenation of the suffix s_n-1 and the prefix s_n-2.

Lets implement the function solve(n, Left, Right), which returns the Fibonacci substring s_n, lying in positions from Left to Right inclusive.

If n = 1 or n = 2, return the corresponding string consisting of one character (s₁ = b, s₂ = a).

Since s_n is a concatenation of the strings s_n-1 and s_n-2, let’s determine which of these parts (s_n-1 or s_n-2) contains the required substring. At the same time, we know the lengths s_n-1 and s_n-2 (this is why we compute the Fibonacci numbers in the fib array).

· If Right ≤ fib(n – 1), then the resulting substring lies entirely in s_n-1. Return solve(n – 1, Left, Right).

· If Left > fib(n – 1), then the resulting substring lies entirely in s_n-2. In this case, you should recompute the indices of the desired substring, namely, subtract the length s_n-1 from Left and Right. Return solve(n – 2, Left – fib(n – 1), Right – fib(n – 1)).

· Otherwise, the resulting substring starts at s_n-1 and ends at s_n-2. You must return the substring from s_n-1 at positions [Left … fib(n – 1)] and concatenate with the substring from s_n-2 at positions [1 … Right – fib(n – 1)]. That is, return solve(n – 1, Left, fib(n – 1)) + solve(n – 2, 1, Right – fib(n – 1)).

Example

Let n = 7, m = 6, l = 7.

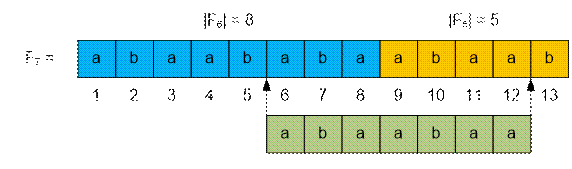
solve(7, 6, 12) = solve(7 – 1, 6, fib(6)) + solve(7 – 2, 1, 12 – fib(6)) =

= solve(6, 6, 8) + solve(5, 1, 4) = “aba” + “abaa” = “abaabaa”.

Algorithm realization

Let’s add the Fibonacci numbers to the fib array: fib[i] contains the length of s_i.

#define MAX 44

int fib[MAX] = {0, 1};

Implement the function solve.

string solve(int n, int Left, int Right)

{

if (n == 1) return "b";

if (n == 2) return "a";

if (Right <= fib[n-1]) return solve(n-1, Left, Right);

if (Left > fib[n-1])

return solve(n-2, Left - fib[n-1], Right - fib[n-1]);

return solve(n-1, Left, fib[n-1]) + solve(n-2, 1, Right - fib[n-1]);

}

The main part of the program. Find the first MAX Fibonacci numbers.

for(int i = 2; i < MAX; i++)

fib[i] = fib[i-1] + fib[i-2];

Read the input data. Find and print the answer.

scanf("%d %d %d",&n,&m,&l);

string res = solve(n,m,m+l-1);

puts(res.c_str());

Java realization

import java.util.*;

public class Main

{

public static int MAX = 44;

public static int fib[] = new int[44];

public static String solve(int n, int Left, int Right)

{

if (n == 1) return "b";

if (n == 2) return "a";

if (Right <= fib[n-1])

return solve(n-1, Left, Right);

if (Left > fib[n-1])

return solve(n-2, Left - fib[n-1], Right - fib[n-1]);

return solve(n-1, Left, fib[n-1]) +

solve(n-2, 1, Right - fib[n-1]);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

fib[1] = 1;

for(int i = 2; i < MAX; i++)

fib[i] = fib[i-1] + fib[i-2];

int n = con.nextInt();

int m = con.nextInt();

int l = con.nextInt();

String res = solve(n,m,m+l-1);

System.out.println(res);

con.close();

}

}