2585. Profit
The cows have opened a new business, and
Farmer John wants to see how well they are doing. The business operates
for n (1 ≤ n ≤ 105) days, and on
each i-th day, the cows record their net profit Pi (-1000 ≤ Pi ≤ 1000).
Farmer John wants to find the maximum
profit that the cows have obtained during any consecutive period of time (note
that a consecutive period of time can have a length from one day to n days).
Help him by writing a program to find the maximum continuous profit.
Input. The first line contains an integer n. Each of
the next n lines contains one integer Pi.
Output. Print the value of the maximum profit obtained during
any consecutive period of time.
|
Sample
input |
Sample
output |
7-349-2-58-3 |
14 |
SOLUTION
sequence processing
Algorithm analysis
In this problem you should find a
subsequence of consecutive numbers that will have the maximum possible sum
among all such subsequences. If the maximum sum is achieved on the subsequence xi, xi+1,
..., xj, then for any k, 1 £ k < i
and l, j < l
£ n, the sum of elements xk, ..., xi-1
and xj+1, ..., xl
will be negative.
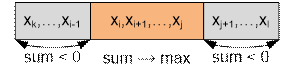
Kadane’s algorithm. Move through the array from left
to right and accumulate the current partial sum in the variable s. If at any moment s becomes
negative, set s = 0. The maximum of all values of the variable s during the traversal of the array will be the answer to
the problem.
Example
For the input sequence the
maximum
profit is 14.
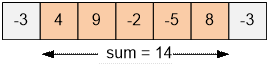
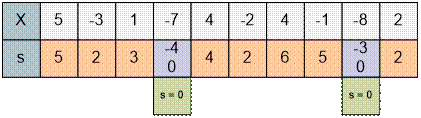
Consider an example of
sequence X. Construct the partial
sums. Reset the current value of the partial sum to zero when the sum becomes less
than zero, and start counting the sum from the next number. The maximum value
among all partial sums is 6, which is the answer. The desired subsequence will
be 4, -2, 4.
Algorithm implementation
Read the length
of the sequence n. Initialize the value of the maximum profit max and the current partial sum s to zero.
scanf("%d",&n);
s = 0; max = 0;
Read n integers. Each read integer Number is added to the current sum s and we
recompute the current value of profit max. If at any step
the value of s becomes negative, set it to zero and continue the process.
for(i = 0; i < n; i++)
{
scanf("%d",&Number);
s += Number;
if (s >
max) max = s;
if (s < 0) s =
0;
}
Print the answer.
printf("%d\n",max);
Java implementation
import java.util.*;
public class Main
{
public static void
main(String[] args)
{
Scanner con = new
Scanner(System.in);
int n = con.nextInt();
int s = 0,
max = 0;
for (int i = 0;
i < n; i++)
{
int val = con.nextInt();
s += val;
if (s >
max) max = s;
if (s <
0) s = 0;
}
System.out.println(max);
con.close();
}
}
Python implementation
Read the length
of the sequence n. Initialize the value of the maximum profit max_profit and the current partial sum s to zero.
n = int(input())
s = 0
max_profit = 0
Read n integers. Each read integer Number is added to the current sum s and we
recompute the current value of profit max_profit. If at any step the value of s becomes negative, set it to zero and
continue the process.
for i in range(n):
Number = int(input())
s
+= Number
if s >
max_profit: max_profit = s
if s < 0: s = 0
Print the answer.
print(max_profit)