2591. Круги с посевами

Бесси и ее друзья из стада стали слишком территориальными. n коров, пронумерованные 1 ... n, собрались на пастбище. Каждая i-ая корова задается точкой в целочисленной системе координат (x_i, y_i) и целочисленным радиусом r_i, характеризующим круг ее занимаемой территории.

Иногда коровы становятся жадными и начинают ходить на территории своих соседей. Вычислите для каждой коровы количество соседей, чьи территории пересекаются с ее.

Рассмотрим пример с шестью коровами и указанными их местами расположения с радиусами территориальных кругов (не путайте радиус с диаметром!):

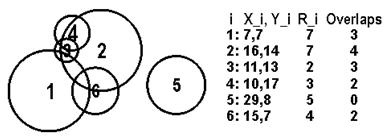
Как показано на рисунке, для каждого круга количество его пересечений с другими кругами подсчитать не сложно.

Замечание: во входных данных отсутствуют случаи касания кругов.

Вход. Первая строка содержит целое число n (1 ≤ n ≤ 400). Каждая из следующих n строк содержит три целых числа x_i, y_i (0 ≤ x_i ≤ 10000, 0 ≤ y_i ≤ 10000) и r_i (1 ≤ r_i ≤ 500).

Выход. Вывести n строк. i-ая строка должна содержать количество кругов, с которыми пересекается поле i-ой коровы.

Пример входа	Пример выхода
6 7 7 7 16 14 7 11 13 2 10 17 3 29 8 5 15 7 4	3 4 3 2 0 2

РЕШЕНИЕ

перебор

Анализ алгоритма

Переберем все пары коров и для каждой коровы подсчитаем количество пересечений ее круга с кругами других коров. Нас интересует лишь факт пересечения кругов, а не координаты точек пересечения.

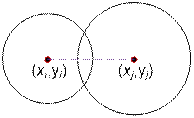
Рассмотрим два круга с параметрами (x_i, y_i, r_i) и (x_j, y_j, r_j). Круги пересекаются, если расстояние между их центрами не больше суммы радиусов. Для избежания работы с действительными числами, возведем указанное неравенство в квадрат:

(x_j – x_i)² + (y_j – y_i)² ≤ (r_i + r_j) ²

Реализация алгоритма

Информацию о корове (координаты центра, радиус и количество пересечений с другими кругами коров) будем хранить в структуре Cow.

#define MAX 400

struct Cow

{

int x, y, r, cnt;

} cows[MAX];

Читаем входные данные.

scanf("%d", &n);

for (i = 0; i < n; i++)

{

scanf("%d %d %d", &cows[i].x, &cows[i].y, &cows[i].r);

Изначально количество пересечений круга коровы i с другими кругами равно 0.

cows[i].cnt = 0;

}

Перебираем все возможные пары коров (i, j), i < j.

for (i = 0; i < n; i++)

{

for (j = i + 1; j < n; j++)

{

Проверяем, пересекаются ли круги коров i и j. Если пересекаются, то увеличим на единицу значения cows[i].cnt и cows[j].cnt.

if ((cows[i].x - cows[j].x) * (cows[i].x - cows[j].x) +

(cows[i].y - cows[j].y) * (cows[i].y - cows[j].y) <=

(cows[i].r + cows[j].r) * (cows[i].r + cows[j].r))

{

cows[i].cnt++;

cows[j].cnt++;

}

}

Все пересечения круга i-ой коровы найдены. Выводим их количество.

printf("%d\n", cows[i].cnt);

}