2824. Удаление дорог

Имеется сеть из n городов и m двунаправленных дорог, соединяющих эти города. Первые k городов считаются важными. Вам необходимо так удалить наименьшее количество дорог, чтобы в оставшейся сети не было циклов, проходящих через важные города. Цикл представляет собой последовательность по крайней мере трех таких разных городов, что каждая пара соседних городов связана между собой дорогой, а первый и последний город также соединены дорогой.

Вход. Первая строка содержит количество тестов t (1 ≤ t ≤ 20).

Каждый тест начинается строкой, содержащей три целых числа n, m и k (1 ≤ n ≤ 10000, 1 ≤ m ≤ 50000, 1 ≤ k ≤ n) – количество городов, дорог и важных городов соответственно. Города пронумерованы числами от 0 до n – 1, а важные города пронумерованы числами от 0 до k – 1. Каждая из следующих m строк содержит два целых числа a_i и b_i, 0 ≤ i < m, описывающих номера разных городов, соединенных дорогой.

Известно, что 0 ≤ a_i, b_i < n и a_i ≠ b_i. Между двумя городами существует не более одной дороги.

Выход. Для каждого теста, пронумерованного числами от 1 до t, вывести строку “Case #i:”, за которой следует целое число – наименьшее количество дорог, подлежащих удалению таким образом, чтобы не осталось ни одного цикла, в который входил хотя бы один важный город.

Пример входа	Пример выхода
2 5 7 2 0 1 1 2 1 4 0 2 2 4 2 3 3 4 8 12 2 0 2 0 4 0 5 2 3 2 7 3 1 3 4 4 6 5 6 5 7 6 1 7 1	Case #1: 2 Case #2: 4

РЕШЕНИЕ

система непересекающихся множеств

Анализ алгоритма

Очевидно, что ребра, не инцидентные важным городам, можно не удалять. Пусть подграф G’, состоящий из неважных вершин и ребер, не инцидентых важным городам, имеет c компонент связности. Рассмотрим граф, состоящий из k + c вершин:

· k вершин, пронумерованных от 0 до k – 1, и соответствующих важным городам;

· c вершин, пронумерованных от k до k + c – 1, соответствующих компонентам связности подграфа G’.

При этом из вершин, соответствующих компонентам связности G’, могут идти мультиребра в важные города.

Несмотря на то, что такой граф не обязательно является связным (это не гарантируется в условии задачи), запустим на нем алгоритм построения минимального остовного дерева, используя систему непересекающихся множеств. Считаем вес каждого ребра равным 1. Подсчитаем количество ребер в нем. Все ребра, не вошедшие в таким образом построенное остовное дерево, и которые являются инцидентными важным городам, следует удалить из исходного графа.

Пример

Рассмотрим первый пример, в котором города 0 и 1 являются важными. Можно удалить дороги (0, 1) и (1, 2), после чего оставшаяся сеть не будет содержать циклов, содержащих важные города.

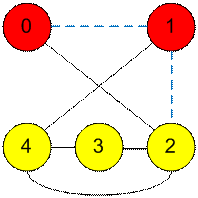
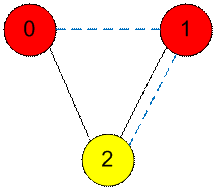
Неважные вершины 2, 3, 4 с учетом ребер (3, 4), (2, 3), (2, 4) (не инцидентных важным вершинам), образуют одну компоненту связности. Стянем их во вторую вершину. Поскольку в исходном графе имеются ребра (1, 4) и (1, 2) то в новом появится мультиребро (1, 2). Для получения остовного дерева (графа без циклов) из результирующего графа следует удалить два ребра.

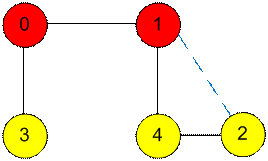
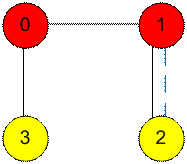
Рассмотрим еще один пример. Слева задан входной граф, справа – стянутый. Пусть k = 2. Неважные вершины с ребрами, не инцидентными важным вершинам, образуют две компоненты связности. Как видно из графа справа, для решения задачи достаточно удалить одно ребро.

Реализация алгоритма

Объявим структуру дороги (ребра) и массив дорог.

struct Edge

{

int u, v;

Edge(int a, int b) {u = a; v = b;}

};

vector<Edge> e;

Функция Repr возвращает представителя множества.

int Repr(int n)

{

if (n == mas[n]) return n;

return mas[n] = Repr(mas[n]);

}

Функция Union объединяет множества, содержащие элементы x и y. Возвращает 1, если x и y принадлежат одному множеству.

int Union(int x,int y)

{

int x1 = Repr(x),y1 = Repr(y);

mas[x1] = y1;

return (x1 == y1);

}

Основная часть программы. Последовательно обрабатываем входные тесты.

scanf("%d", &tests);

while(tests--)

{

scanf("%d %d %d", &n, &m, &k);

mas.resize(n, 0); e.clear();

Построим систему непересекающихся множеств из вершин графа.

for(i = 0; i < n; i++) mas[i] = i;

Неважные вершины, соединенные ребром, будем объединять в одно множество. В массив e занесем ребра, инцидентные важным городам.

for(i = 0; i < m; i++)

{

scanf("%d %d", &a, &b);

if ((a >= k) && (b >= k)) Union(a,b);

else e.push_back(Edge(a,b));

}

В переменной res подсчитаем количество ребер, инцидентных важным вершинам, и которые не попали в остовное дерево. Это значение и будет ответом задачи.

for(res = i = 0; i < e.size(); i++)

res += Union(e[i].u,e[i].v);

printf("Case #%d: %d\n",cs++,res);

}