230. Парад скобок

Посчитайте количество различных правильных скобочных последовательностей, состоящих из k₁ пар скобок первого типа, k₂ пар скобок второго типа, …, k_m пар скобок m-го типа. Последовательность скобок считается правильной в следующих случаях:

• Пустая последовательность – правильная;

• Если A и B – правильны, то AB – тоже правильная

• Если A – правильная, то (iA)i – правильная, где (i и )i – открывающая и закрывающая скобка одного типа.

Вход. Первая строка содержит количество тестов 0 < n ≤ 1000. Каждая из следующих n строк описывает тест. Каждая строка начинается с числа 0 < m ≤ 100 – количества различных типов скобок. Затем m положительных чисел k₁, k₂, …, k_m следуют одно за другим через пробел. Число k_i – это количество пар скобок i-го типа. Общее количество пар скобок – не больше 1000.

Выход. Для каждого теста выведите строку, содержащую одно целое число – ответ задачи по модулю 1000000007.

Пример входа	Пример выхода
3 1 4 2 2 2 3 1 2 3	14 84 7920

РЕШЕНИЕ

числа Каталана

Анализ алгоритма

Будем говорить, что скобка имеет i-ый тип, если она покрашена краской номер i. Пусть изначально все скобки не покрашены. Тогда изначально имеется s = пар скобок, из которых можно составить Cat(s) правильных скобочных последовательностей. Здесь через Cat(s) обозначено s-ое число Каталана.

Покрасить первой краской мы должны k₁ пару скобок, которые можно выбрать способами. k₂ пары скобок, которые следует покрасить второй краской, можно выбрать способами. И так далее, для покраски i-ой краской можно выбрать пары скобок способами.

Количество искомых различных правильных скобочных последовательностей равно произведению

Cat(s) * * * … * * … * ,

взятому по модулю1000000007 . Заметим, что последний множитель в произведении равен 1, так как

= = 1

Пример

Для второго теста s = 4 и ответ равен Cat(4) * * = 14 * 6 * 1 = 84.

Для третьего теста s = 6 и ответ равен Cat(6) * * * = 132 * 6 * 10 * 1 = 7920.

Реализация алгоритма

Объявим макросы и необходимые массивы. В ячейках массива cat будем вычислять числа Каталана, в ячейках cnk – биномиальные коэффициенты. Входные значения k_i запоминаем в массиве k.

#define MD 1000000007

#define MAX 1001

long long k[MAX], cat[MAX];

long long cnk[MAX][MAX];

Функция c вычисляет значение биномиального коэффициента и запоминает его в ячейке cnk[n][k].

long long c(int n, int k)

{

Если cnk[n][k] > 0, то значение было вычислено ранее. Следует его просто вернуть.

if (cnk[n][k] > 0) return cnk[n][k];

Поскольку = , то если при n – k < k вместо находить , то время вычисления биномиального коэффициента уменьшится.

if (n - k < k) return c(n,n-k);

Если k = 0, то значение равно 1.

if (!k) return cnk[n][k] = 1;

Для вычисления биномиального коэффициента используем рекуррентное соотношение

= +

return cnk[n][k] = (c(n-1,k) + c(n-1,k-1)) % MD;

}

Основная часть программы. В массиве cat вычисляем числа Каталана исходя из рекуррентной формулы сat_i = 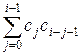. Вычисления проводим по модулю MD = 1000000007.

cat[0] = cat[1] = 1;

for(i = 2; i < 1001; i++)

{

for(j = 0; j < i; j++)

cat[i] = (cat[i] + cat[j] * cat[i-j-1]) % MD;

}

Читаем входные данные. В переменной s вычисляем сумму .

scanf("%d",&n);

while(n--)

{

scanf("%d",&m);

for(s = 0, i = 1; i <= m; i++)

scanf("%d",&k[i]), s += k[i];

Положим сначала результат res равным Cat(s).

res = cat[s];

Умножаем значение res на для всех i от 1 до m.

for(i = 1; i <= m; i++)

res = (res * c(s,k[i])) % MD, s -= k[i];

Выводим результат.

printf("%lld\n",res);

}