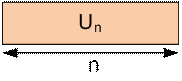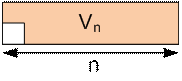236. Triomino
In how many ways can you tile a 2 × n
rectangle with triominoes? A triomino is a geometric shape made from three
squares joined along complete edges. There are only two possible triominoes:
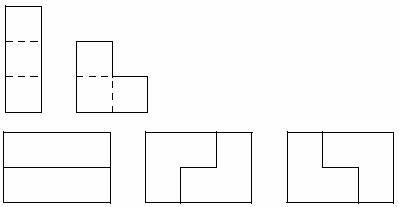
For example, you can tile a 2 × 3
rectangle only in 3 different ways. As the answer can be quite big, you just
need to find the number of ways modulo 106.
Input. The first line contains the number of test
cases t (1 ≤ t ≤ 100). Each of the following t
lines contains the value of n (0 < n < 109).
Output. For each test case print in a separate
line a number of ways you can tile a 2 × n rectangle. Print the
answer modulo 106.
Sample
input
3
3
4
6
Sample
output
3
0
11
SOLUTION
combinatorics
Algorithm analysis
Let Un
be the number of ways to tile a 2 × n
rectangle. Let Vn be
the number of ways to tile a 2 × n rectangle
without a corner 1 × 1.
We have the following initial relations:
U1= 0, U2 = 0, U3
= 3
V1 = 0, V2 = 1, V3
= 0
Consider all possible ways to tile the
rectangles Un and Vn.
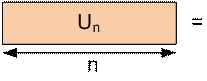
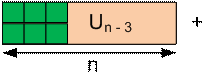
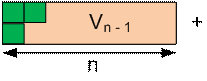
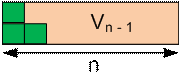
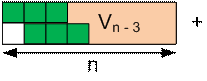
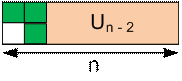
We get the next relations:
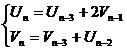
Based on the initial conditions, we find U0 and V0:
, 
, 
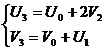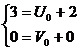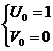
Create a table of values Un
and Vn:
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
Un |
1 |
0 |
0 |
3 |
0 |
0 |
11 |
0 |
0 |
41 |
0 |
0 |
153 |
|
Vn |
0 |
0 |
1 |
0 |
0 |
4 |
0 |
0 |
15 |
0 |
0 |
56 |
0 |
Shift the second line two places left. Then
the columns for indexes not divisible by 3, will contain only zeros. Delete
them. Number the new columns. The table takes the form:
|
n |
0 |
1 |
2 |
3 |
4 |
|
Un |
1 |
3 |
11 |
41 |
153 |
|
Vn |
1 |
4 |
15 |
56 |
209 |
Rewrite the recurrence relations in the
form:
, 
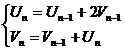Or the same as
,
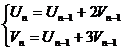Consider the matrix A = 
. A2
= 
, A3
= 
. You can notice that the first row of the matrix An contains the
values of Un-1 and
Vn-1. To solve
the problem (to find the value of Un)
it is sufficient to calculate the An+1 and print the
element in its upper left corner. Make the exponentiation in O(log2n)
time because n
< 109. All calculations are carried out modulo 106.
Algorithm
realization
Declare a modulus MOD under which we perform calculations. Declare a
two-dimensional matrix structure matrix.
#define MOD 1000000
struct matrix
{
long long
a, b, c, d;
matrix(long long
_a = 1, long long
_b = 0,
long long _c = 0, long long _d = 1)
{a = _a; b = _b; c = _c; d = _d;}
};
The function mult returns the product of matrices x and y.
matrix mult(matrix x, matrix y)
{
matrix res;
res.a = (x.a * y.a + x.b * y.c) % MOD;
res.b = (x.a * y.b + x.b * y.d) % MOD;
res.c = (x.c * y.a + x.d * y.c) % MOD;
res.d = (x.c * y.b + x.d * y.d) % MOD;
return res;
}
Raise a matrix m to the power of n.
matrix pow(matrix m, long long n)
{
matrix res = matrix();
while(n > 0)
{
if (n & 1) res = mult(res,m);
n >>= 1;
m = mult(m,m);
}
return res;
}
Raise a matrix to the power of n.
long long Solve(long long n)
{
matrix res = matrix(1,1,2,3);
res = pow(res,n);
return res.a;
}
The main part of the program. Read the
input data. If n is not divisible by
3, the answer is 0. Otherwise divide n
by 3 and raise the matrix to the power of n + 1.
scanf("%d",&tests);
while(tests--)
{
scanf("%d",&n);
if (n % 3)
{
printf("0\n"); continue;
}
n /= 3;
res = Solve(n+1);
printf("%d\n",res);
}
return 0;
}