263. Три единицы

Вычислить количество последовательностей длины n, состоящих только из нулей и единиц, в которых не встречается три единицы подряд.

Вход. Длина последовательностей n (1 ≤ n ≤ 10⁵).

Выход. Вывести количество искомых последовательностей по модулю 12345.

Пример входа	Пример выхода
4	13

РЕШЕНИЕ

динамическое программирование

Анализ алгоритма

Обозначим через f(n) количество искомых последовательностей из 0 и 1 длины n. Если на первом месте последовательности будет находиться 0, то начиная со второго места можно построить f(n – 1) последовательность. Если на первом месте стоит 1, то на втором месте возможны оба варианта. Если там стоит 0, то на следующих n – 2 свободных местах можно построить f(n – 2) последовательности. Если 1, то на третьем месте обязательно должен находиться 0 и начиная с четвертого места можно построить f(n – 3) последовательности.

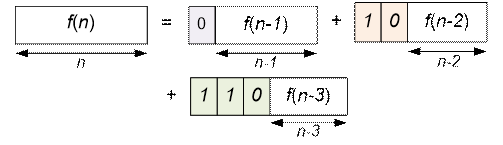
Имеем рекуррентное соотношение: f(n) = f(n – 1) + f(n – 2) + f(n – 3). Остается вычислить начальные значения:

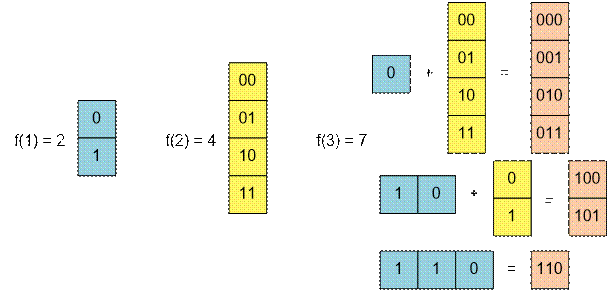
· f(1) = 2, так как существует две последовательности длины 1: 0 и 1.

· f(2) = 4, так как существует четыре последовательности длины 2: 00, 01, 10 и 11.

· f(3) = 7, так как существует семь последовательностей длины 3: 000, 001, 010, 011, 100, 101 и 110.

Пример

Реализация алгоритма

Объявим массив f, в котором будем сохранять значения f(1), f(2), …, f(n).

int f[100010];

Читаем входное значение n.

scanf("%d",&n);

Заносим в соответствующие ячейки массива f значения f(1), f(2) и f(3).

f[1] = 2; f[2] = 4; f[3] = 7;

Вычисляем значения f(i) по рекуррентной формуле. Вычисления производим по модулю 12345.

for(i = 4; i <= n; i++)

f[i] = (f[i-1] + f[i-2] + f[i-3]) % 12345;

Выводим ответ.

printf("%d\n",f[n]);

Реализация алгоритма – рекурсия + запоминание

Объявим массив dp для запоминания результатов: dp[i] будет хранить значение f(i).

int dp[100001];

Реализуем функцию f(n) – количество искомых последовательностей из 0 и 1 длины n. Используем технику мемоизации.

int f(int n)

{

if (n == 1) return 2;

if (n == 2) return 4;

if (n == 3) return 7;

if (dp[n] != -1) return dp[n];

return dp[n] = (f(n-1) + f(n-2) + f(n-3)) % 12345;

}

Основная часть программы. Читаем входное значение n.

scanf("%d",&n);

Инициализируем массив dp.

memset(dp,-1,sizeof(dp));

Вычисляем и выводим значение f(n).

printf("%d\n",f(n));

Java реализация

import java.util.*;

public class Main

{

public static int MAX = 100010;

static int f[] = new int[MAX];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

f[1] = 2; f[2] = 4; f[3] = 7;

for(int i = 4; i <= n; i++)

f[i] = (f[i-1] + f[i-2] + f[i-3]) % 12345;

System.out.println(f[n]);

con.close();

}

}

Python реализация

Читаем входное значение n.

n = int(input())

Инициализируем список dp. Заносим в соответствующие ячейки списка значения f(1), f(2) и f(3).

dp = [0] * (n + 4)

dp[1], dp[2], dp[3] = 2, 4, 7

Вычисляем значения dp[i] = f(i) по рекуррентной формуле. Вычисления проводим по модулю 12345.

for i in range(4, n + 1):

dp[i] = (dp[i-1] + dp[i-2] + dp[i-3]) % 12345;

Выводим ответ.

print(dp[n])

Python реализация – рекурсия с запоминанием

Увеличим стек для рекурсии.

import sys

sys.setrecursionlimit(10000)

Реализуем функцию f(n) – количество искомых последовательностей из 0 и 1 длины n. Используем технику мемоизации.

def f(n):

if n == 1: return 2

if n == 2: return 4

if n == 3: return 7

if dp[n] != -1: return dp[n]

dp[n] = (f(n - 1) + f(n - 2) + f(n - 3)) % 12345

return dp[n]

Основная часть программы. Читаем входное значение n.

n = int(input())

Инициализируем список dp.

dp = [-1] * 100001

Вычисляем и выводим значение f(n).

print(f(n))