263. Three ones

Find the number of sequences of length n, consisting only of zeros and ones, that do not have three one’s in a row.

Input. The length of the sequences n (1 ≤ n ≤ 10⁵).

Output. Print the required number of sequences modulo 12345.

Sample input	Sample output
4	13

SOLUTION

dynamic programming

Algorithm analysis

Let f(n) be the number of required sequences consisting of 0 and 1 of length n. If the first number in the sequence is 0, then starting from the second place we can build f(n – 1) sequences. If the first number in the sequence is 1, then second number can be any (0 or 1). If second number is 0, on the next n – 2 free places we can construct f(n – 2) sequences. If second number is 1, the third number must be exactly 0, and starting from the forth place we can construct f(n – 3) sequences.

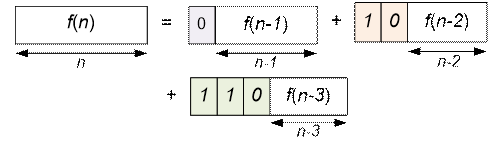
We have the recurrence: f(n) = f(n – 1) + f(n – 2) + f(n – 3). Now we must calculate the initial values:

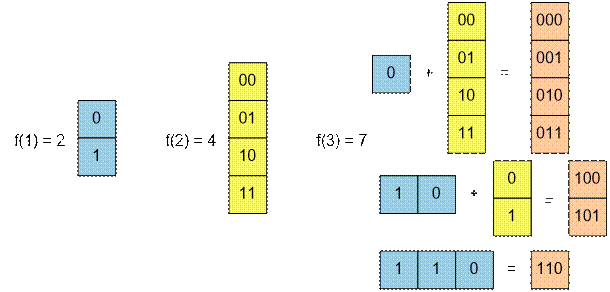
f(1) = 2, since there are two sequence of lengths 1: 0 and 1.

f(2) = 4, since there are four sequence of lengths 2: 00, 01, 10 and 11.

f(3) = 7, since there are seven sequence of lengths 3: 000, 001, 010, 011, 100, 101 and 110.

Example

Algorithm realization

Declare an array f where we shall store the values f(1), f(2), …, f(n).

int f[100010];

Read the input value of n.

scanf("%d",&n);

Store the values of f(1), f(2) and f(3) into corresponding cells of array f.

f[1] = 2; f[2] = 4; f[3] = 7;

Compute the values f(i) according to recurrence formula. Calculations are made by modulo 12345.

for(i = 4; i <= n; i++)

f[i] = (f[i-1] + f[i-2] + f[i-3]) % 12345;

Print the answer.

printf("%d\n",f[n]);

Algorithm realization – recursion + memorization

Declare an array dp to store the results: dp[i] stores the value of f(i).

int dp[100001];

Implement the function f(n), the required number of sequences of 0 and 1 of length n. Use the memoization technique.

int f(int n)

{

if (n == 1) return 2;

if (n == 2) return 4;

if (n == 3) return 7;

if (dp[n] != -1) return dp[n];

return dp[n] = (f(n-1) + f(n-2) + f(n-3)) % 12345;

}

The main part of the program. Read the input value of n.

scanf("%d",&n);

Initialize a dp array.

memset(dp,-1,sizeof(dp));

Compute and print the answer f(n).

printf("%d\n",f(n));

Java realization

import java.util.*;

public class Main

{

public static int MAX = 100010;

static int f[] = new int[MAX];

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

f[1] = 2; f[2] = 4; f[3] = 7;

for(int i = 4; i <= n; i++)

f[i] = (f[i-1] + f[i-2] + f[i-3]) % 12345;

System.out.println(f[n]);

con.close();

}

}

Python realization

Read the input value of n.

n = int(input())

Initialize the dp list. Store the values of f(1), f(2) and f(3) into the corresponding cells of the list.

dp = [0] * (n + 4)

dp[1], dp[2], dp[3] = 2, 4, 7

Compute the values dp[i] = f(i) according to recurrence formula. Calculations are made by modulo 12345.

for i in range(4, n + 1):

dp[i] = (dp[i-1] + dp[i-2] + dp[i-3]) % 12345;

Print the answer.

print(dp[n])

Python realization – recursion with memoization

Increase stack for recursion.

import sys

sys.setrecursionlimit(10000)

Implement the function f(n), the required number of sequences of 0 and 1 of length n. Use the memoization technique.

def f(n):

if n == 1: return 2

if n == 2: return 4

if n == 3: return 7

if dp[n] != -1: return dp[n]

dp[n] = (f(n - 1) + f(n - 2) + f(n - 3)) % 12345

return dp[n]

The main part of the program. Read the input value of n.

n = int(input())

Initialize a dp list.

dp = [-1] * 100001

Compute and print the answer f(n).

print(f(n))