273. Возведение в степень

По трем натуральным числам x, n и m вычислите значение xⁿ mod m.

Вход. Три натуральных числа x, n, m (1 ≤ x ≤ 10⁹, 1 ≤ n ≤ 10⁷, 2 ≤ m ≤ 10⁹).

Выход. Выведите одно число – значение xⁿ mod m.

Пример входа	Пример выхода
2 3 100	8

РЕШЕНИЕ

возведение в степень

Анализ алгоритма

Возведение в степень – это математическая операция, обозначаемая как xⁿ, которая включает два числа: основание x и показатель степени n. Если n –натуральное число, то операция возведения в степень сводится к последовательному умножению основания на само себя: xⁿ – это произведение n множителей, каждый из которых равен x: xⁿ = x * x * … * x.

Как вычислить xⁿ по заданным x и n? Можно воспользоваться одним циклом со сложностью O(n). Линейный алгоритм пройдет по времени, так как n ≤ 10⁷.

Можно также воспользоваться быстрым возведением в степень:

xⁿ =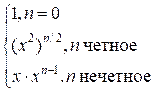

Реализация алгоритма

Воспользуемся 64 битовым целочисленным типом long long. Читаем входные данные.

scanf("%lld %lld %lld",&x,&n,&m);

Вычисляем значение xⁿ mod m при помощи цикла.

res = 1;

for(i = 1; i <= n; i++)

res = (res * x) % m;

Выводим ответ.

printf("%lld\n",res);

Реализация с помощью быстрого возведения в степень

Функция PowMod вычисляет значение выражения xⁿ mod m.

long long PowMod(long long x, long long n, long long m)

{

if (n == 0) return 1;

if (n % 2 == 0) return PowMod((x * x) % m, n / 2, m);

return (x * PowMod(x, n - 1, m)) % m;

}

Основная часть программы. Читаем входные данные.

scanf("%lld %lld %lld",&x,&n,&m);

Вычисляем и выводим ответ.

res = PowMod(x,n,m);

printf("%lld\n",res);

Реализация с помощью классов

#include <stdio.h>

class Long

{

private:

long long value;

public:

static long long mod;

Long() : value(0) {}

Long(long long value) : value(value) {}

void Read(void)

{

scanf("%lld",&value);

}

static void ReadMod(void)

{

scanf("%lld",&mod);

}

void Print(void)

{

printf("%lld\n",value);

}

bool IsOdd(void)

{

return value & 1;

}

Long operator* (const Long &x)

{

return (value * x.value) % mod;

}

Long operator/ (const long long &x)

{

return value / x;

}

bool operator== (const long long &x)

{

return this->value == x;

}

Long operator^ (Long n)

{

Long x(*this);

if (n == 0) return Long(1);

if (n.IsOdd()) return x * ((x * x) ^ (n/2));

return (x * x) ^ (n/2);

}

};

long long Long::mod = 0;

int main(void)

{

Long x, n, res;

x.Read();

n.Read();

Long::ReadMod();

res = x ^ n;

res.Print();

return 0;

}

Java реализация – линейная сложность

import java.util.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

long x = con.nextLong(),

n = con.nextLong(),

m = con.nextLong();

long res = 1;

for(int i = 1; i <= n; i++) res = (res * x) % m;

System.out.println(res);

con.close();

}

}

Java реализация – O(log₂n)

import java.util.*;

public class Main

{

static long PowMod(long x, long n, long m)

{

if (n == 0) return 1;

if (n % 2 == 0) return PowMod((x * x) % m, n / 2, m);

return (x * PowMod(x, n - 1, m)) % m;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

long x = con.nextLong();

long n = con.nextLong();

long m = con.nextLong();

long res = PowMod(x,n,m);

System.out.println(res);

con.close();

}

}

Java реализация – powMod

import java.util.*;

import java.math.*;

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

BigInteger x = con.nextBigInteger();

BigInteger n = con.nextBigInteger();

BigInteger m = con.nextBigInteger();

System.out.println(x.modPow(n,m));

con.close();

}

}

Java реализация (работа с входными/выходными файлами)

import java.io.*;

import java.util.*;

public class Main

{

public static void main(String[] args) throws IOException

{

//Scanner con = new Scanner(System.in);

Scanner con = new Scanner(new FileReader ("273.in"));

PrintWriter out = new PrintWriter(new File("273.out"));

long x = con.nextLong(),

n = con.nextLong(),

m = con.nextLong();

long res = 1;

for(int i = 1; i <= n; i++) res = (res * x) % m;

//System.out.println(res);

out.println(res);

out.flush();

out.close();

}

}

Python реализация – pow

Читаем входные данные.

x, n, m = map(int, input().split())

Вычисляем и выводим ответ. Используем встроенную функцию pow для вычисления выражения xⁿ mod m.

print(pow(x, n, m))

Python реализация – цикл

Читаем входные данные.

x, n, m = map(int, input().split())

Вычисляем значение xⁿ mod m при помощи цикла.

res = 1

for i in range(1, n + 1):

res = (res * x) % m

Выводим ответ.

print(res)