279. Телепорты

Вы участвуете в соревновании по пересечению Египта с запада на восток по прямолинейному отрезку. Вначале вы располагаетесь в западном конце отрезка. По правилам соревнования вы должны двигаться только по отрезку и только на восток.

На отрезке есть n телепортов. Телепорт задается двумя точками на отрезке. Всякий раз, когда вы достигаете одной из этих точек, телепорт немедленно телепортирует вас в другую точку (следует заметить, что в зависимости от того, какой точки вы достигли, телепорт может отправить вас как на восток, так и на запад от вашего текущего положения). После телепортирования вы должны продолжать двигаться на восток вдоль отрезка. Вы не можете избежать точек телепортов, которые находятся на вашем пути. Нет двух точек телепортов с одинаковой позицией. Все точки телепортов находятся строго между началом и концом отрезка.

Каждый раз, когда вы телепортируетесь, вы получаете один балл. Цель соревнования – получить как можно больше баллов. Чтобы максимизировать баллы, которые вы получаете, вам разрешено добавить на отрезке не более m новых телепортов перед началом вашего путешествия. При использовании новых телепортов вы также получаете баллы.

Вы можете поставить точки новых телепортов везде, где хотите (даже в нецелых позициях), но так, чтобы они не занимали позиции, уже занятые другими точками телепортов, то есть, позиции всех точек, принадлежащих всем телепортам, должны быть различными. Точки новых телепортов также должны лежать строго между началом и концом отрезка.

Следует заметить, что гарантируется, что вне зависимости от способа добавления телепортов, всегда можно достичь конца отрезка.

Напишите программу, которая по заданным позициям точек для n телепортов и количеству m новых телепортов, которые вы можете добавить, вычисляет максимальное количество баллов, которые можно получить в итоге.

Вход. Первая строка содержит количество телепортов n (1 ≤ n ≤ 10⁶), изначально имеющихся на отрезке.

Вторая строка содержит максимальное количество m (1 ≤ m ≤ 10⁶) новых телепортов, которые можно добавить.

Каждая из последующих n строк описывает один телепорт, при этом i-ая из этих строк описывает i-ый телепорт. Каждая строка состоит из двух целых чисел w_i и e_i (1 ≤ w_i, e_i ≤ 2*10⁶), разделенных пробелом. Эти числа представляют собой расстояния от начала отрезка до западной и восточной точки телепорта соответственно.

Никакие две точки заданных телепортов не расположены в одной позиции. Отрезок, по которому вам нужно будет передвигаться, начинается с позиции 0 и заканчивается в позиции 2000001.

Выход. Вывести одно целое число – максимальное количество баллов, которые можно заработать.

Пример входа 1

3

1

10 11

1 4

2 3

Пример выхода 1

6

Пример входа 2

3

3

5 7

6 10

1999999 2000000

Пример выхода 2

12

РЕШЕНИЕ

графы, связность - жадность

Анализ алгоритма

Докажем, что всегда можно добраться с левого конца отрезка на правый, не попав в бесконечный цикл. Построим ориентированный граф, вершинами которого будут отрезки между телепортами.

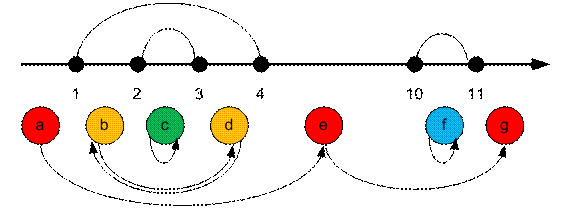
Каждая вершина (кроме последней) имеет исходящее ребро. Идем в правый конец отрезка и смотрим куда нас переносит телепорт.

Каждая вершина (кроме первой) имеет входящее ребро. Мы обязательно попадем по некоторому телепорту в левый конец отрезка.

Первая вершина имеет исходящее ребро, но не имеет входящего. Отправившись в путь, мы никогда не попадем в цикл. И обязательно дойдем до последней, которая имеет входящее ребро, но не имеет исходящего. Таким образом граф представляет собой один путь и множество непересекающихся циклов.

Рассмотрим, что произойдет с добавлением нового телепорта.

1. Телепорт соединяет два отрезка разных компонент связности. Каждый из двух отрезков разбиваются на два (из одной вершины становится две). Если соединить путь и цикл, то получится больший путь. Если соединить два цикла, то получится один больший цикл.

2. Телепорт соединяет два отрезка одной и той же компоненты. Тогда один цикл разобьется на два.

3. Телепорт построен внутри одного отрезка. Цикл (путь) увеличивает свою длину на 1, а также появляется цикл длины один (вершина, указывающая сама на себя).

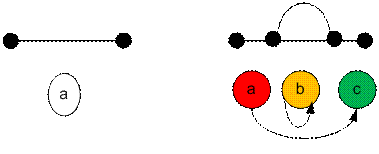
Получим жадный алгоритм:

· Ищем компоненты связности графа, выделяем среди них путь.

· Сортируем циклы по убыванию их размеров.

· Добавим к пути цикл наибольшей длины – таким образом мы увеличим путь.

· Продолжаем добавлять циклы в порядке убывания их размеров пока не останется ни одного цикла. На этом этапе весь граф превратится в один путь.

· Если мы еще не использовали все возможные m телепортов – по очереди применяем шаги 3 и 1. Увеличиваем путь на единицу, получая при этом тривиальный цикл (шаг 3). Затем сливаем этот тривиальный цикл с путем, получая более длинный путь (шаг 1).

Все указанные операции можно совершить за линейное время (сортировку можно совершить подсчетом).

Реализация алгоритма