292. Медведь Миша
Медведь Миша нашел маленькое
сокровище – спрятанный горшочек меда! Он c удовольствием поедал мед, но вдруг
одна пчела его заметила и забила тревогу. Миша знает, что после этого пчелы
вылетят из своих ульев и будут разлетаться вокруг, чтобы настичь его. Он знает,
что нужно бросать горшочек и быстро идти домой, но мед так сладок, что Миша не
хочет бросать его есть слишком рано. Помогите Мише определить последний
возможный момент, когда он может прекратить есть мед.
Лес представлен картой в виде
квадратной сетки, которая состоит из n×n единичных ячеек, стороны которых
параллельны направлениям «север-юг» и «запад-восток». Каждая ячейка леса занята
либо деревом, либо травой, либо ульем, либо Мишиным домом. Две ячейки
называются смежными, если одна из них находится непосредственно к северу, югу,
востоку или западу от другой, но не по диагонали. Миша неповоротлив, поэтому он
может перемещаться только в смежную ячейку. Миша может перемещаться только по
ячейкам с травой и не может перемещаться по ячейкам с деревьями или ульями.
Также он не может перемещаться больше, чем на s ячеек в минуту.
В момент, когда прозвучала
тревога, Миша находится в ячейке с травой, где он нашел горшочек с медом, а все
пчелы – в ячейках, где расположены ульи (в лесу может быть больше одного улья).
С этого момента, на протяжении каждой следующей минуты происходят следующие
события в таком порядке:
·
Если Миша все еще ест мед, он решает, будет ли он
продолжать есть или будет уходить. Если он продолжает есть мед – он не
перемещается всю минуту. Иначе, он немедленно уходит и перемещается по лесу не
более чем на s ячеек, как описано
выше. Миша не может брать с собой мед, и как только он ушел, он уже не может
его есть.
·
Как только Миша заканчивает есть или перемещаться в
течение минуты, пчелы разлетаются на одну ячейку дальше, занимая только ячейки
с травой. Точнее, пчелы разлетаются во все ячейки с травой, смежные с любой
ячейкой, где уже есть пчелы. Как только в ячейке появляются пчелы, они там
остаются навсегда (пчёлы не перемещаются, а распространяются).
Другими словами, пчелы
разлетаются так: когда звучит тревога, пчелы находятся в ячейках, где
расположены ульи. В конце первой минуты они занимают все ячейки с травой,
смежные с ульями, и остаются в тех ячейках, где расположены ульи. В конце
второй минуты пчелы дополнительно занимают все ячейки с травой, смежные со
смежными с ульями ячейками, и так далее. Имея достаточно времени, пчелы займут
все ячейки с травой, которые они могут достичь.
Ни Миша, ни пчелы не могут
покидать пределы леса. Также обратите внимание, что согласно описанным
правилам, Миша ест мед целое число минут.
Пчелы настигают Мишу, если в
какой-то момент времени Миша оказывается в ячейке, занятой пчелами.
Напишите программу, которая по
карте леса определяет наибольшее количество минут, на протяжении которых Миша
может продолжать есть мед в своем исходном расположении, все еще имея
возможность попасть домой до того, как пчелы его настигнут.
Вход. Первая
строка содержит два целых числа – размер (длина стороны) карты леса n (1 ≤ n ≤ 800) и максимальное количество перемещений s (1 ≤ s ≤ 1,000), которые может делать Миша в каждую минуту,
разделенные пробелом.
Последующие
n строк задают карту леса. Каждая из
этих строк содержит n символов,
каждый символ задает одну ячейку на сетке. Возможные символы и их значения
описаны ниже:
T обозначает ячейку с деревом
G обозначает ячейку с травой
M обозначает начальное
расположение Миши и горшочка меда в ячейке с травой
D обозначает ячейку, где
расположен Мишин дом, в который Миша может попасть, а пчелы не могут
H обозначает ячейку с ульем
ПРИМЕЧАНИЕ:
Гарантируется, что карта леса содержит ровно одну букву M, ровно одну букву D и,
по крайней мере, одну букву H. Также
гарантируется, что существует последовательность смежных ячеек G, которые соединяют ячейку с начальным
расположением Миши и ячейку, где расположен Мишин дом, так же как и
последовательность смежных ячеек G,
которые соединяют хотя бы одну из ячеек с ульем с ячейкой с горшочком (то есть,
с ячейкой с Мишиным начальным расположением). Последовательности могут быть и с
длиной, равной нулю, в случае, если ячейка с Мишиным домом или ячейка с ульем
являются смежными с ячейкой с начальным расположением Миши. Также заметьте, что
пчелы не могут распространяться через ячейку с Мишиным домом. Для пчел она –
как ячейка с деревом.
Выход. Одно
целое число – максимально возможное количество минут, на протяжении которых
Миша может продолжать есть мед в начальном расположении, имея возможность
безопасно вернуться домой.
Если
Миша не имеет возможность вернуться домой до того, как пчелы его настигнут,
ваша программа должны выводить отрицательное число -1.
Пример входа 1
7 3
TTTTTTT
TGGGGGT
TGGGGGT
MGGGGGD
TGGGGGT
TGGGGGT
THHHHHT
Пример выхода 1
1
Пример входа 2
7 3
TTTTTTT
TGGGGGT
TGGGGGT
MGGGGGD
TGGGGGT
TGGGGGT
TGHHGGT
Пример выхода 2
2
РЕШЕНИЕ
графы – поиск в ширину
Анализ алгоритма
Будем считать, что медведь
передвигается между двумя соседними клетками за 1 минуту, а пчелы за s
минут. Так мы отобразим тот факт, что скорость движения Миши в s раз
больше скорости пчел. Пусть 1 минута = s единиц времени. Далее все
вычисления будем производить в единицах времени.
При помощи поиска в ширину построим
массив bees распространения пчел по лесу: bees[i][j] содержит
наименьшее время, через которое пчелы будут в точке (i, j).
Очевидно, что bees[i][j] = 0, если в точке (i, j)
находится улей с пчелами.
Пусть медведь закончит есть мед
через x минут (x * s единиц времени). Определим, сможет ли
он добежать до дома, не будучи ужаленным пчелами. В ячейке mecho[i][j]
при помощи поиска в ширину находим наименьшее время, за которое медведь сможет
добраться от горшочка с медом до точки (i, j). Значение x ищем при
помощи бинарного поиска.
Пример
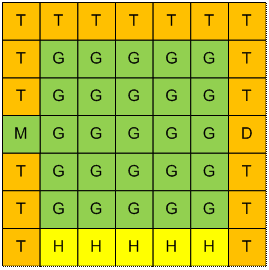
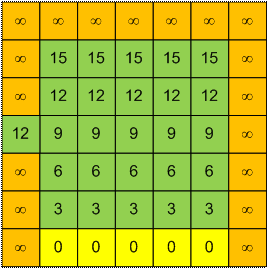
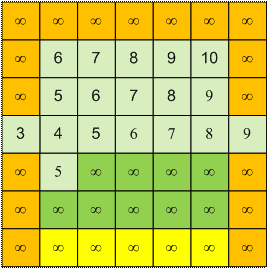
Рассмотрим первый пример. Дом
медведя (D) считаем деревом (пчелы не могут в него попасть), а начальное
расположение Миши (M) травой. Справа на рисунке в каждой ячейке указано
минимальное время, через которое в этой ячейке будут пчелы.
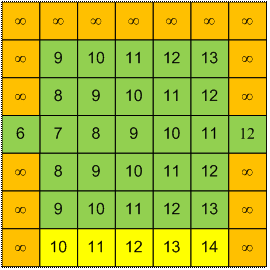
Пусть медведь будет продолжать
есть мед 2 минуты. Тогда он начнет бежать домой в момент времени 2 * 3 = 6. В
каждой ячейке на рисунке слева укажем минимальное время, через которое в этой
ячейке сможет находиться медведь. В ячейках массива mecho (рисунок справа)
учтем тот факт, что медведь не может зайти в ячейку, в которой уже находятся
пчелы. Установим mecho[i][j] = µ,
если в точку (i, j) медведь попасть не может (в ней или
находится дерево, или пчелы достигают эту точку не позже медведя).
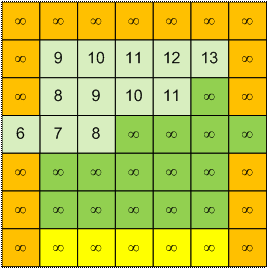
Пусть медведь будет продолжать
есть мед 1 минуту. На следующем рисунке отобразим на ячейках время, за которое
медведь их сможет достичь, не будучи ужаленным пчелами. В этом случае Миша
сможет спрятаться от пчел в своем домике.
Для первого теста ответ будет 1.
Если медведь будет продолжать есть мед две минуты, то скрыться дома он уже не
успеет. А если медведь будет продолжать есть мед одну минуту, то у него есть
шанс скрыться от пчел.
Реализация
алгоритма
Карту
леса храним в массиве m.
#define MAX 810
char m[MAX][MAX];
Массив bees хранит время
распространения пчел: bees[i][j] хранит
наименьшее время, через которое пчелы будут в точке (i, j). Если
пчелы не могут попасть в точку (i, j), то положим bees[i][j]
= µ. Массивы DequeX и DequeY используем для поиска в ширину. Массив mecho используется для
моделирования движения медведя (mecho[i][j] содержит наименьшее время, за которое
медведь успеет добежать от горшочка с медом в точку (i, j)).
int DequeX[MAX*MAX], DequeY[MAX*MAX];
int bees[MAX][MAX], mecho[MAX][MAX];
Добавляем пчелу в точку (i, j), прилетевшую
сюда во время time. Если координаты (i, j) выходят за
границы леса, или точке (i, j) соответствует не трава, или в точку
(i, j) пчелы прилетели раньше (bees[i][j] ≤ time),
то выходим из функции. Иначе добавляем координаты точки (i, j) в
очередь (DequeX[len], DequeY[len]) и устанавливаем значение bees[i][j]
равным time.
void AddBee(int
i, int j, int
time)
{
if ((i < 0)
|| (j < 0) || (i >= n) || (j >= n)) return;
if
((m[i][j] != 'G') ||
(bees[i][j] <= time)) return;
DequeX[len] = i; DequeY[len++] = j;
bees[i][j] = time;
}
Моделируем распространение пчел поиском в ширину. Пчелы
перелетают из одной клетки в соседнюю за время s. Изначально пчелы
находятся только в ульях.
void FillBees(void)
{
int i, j, k,
time;
for(k = 0; k
< len; k++)
{
i = DequeX[k]; j = DequeY[k]; time =
bees[i][j] + s;
AddBee(i-1,j,time); AddBee(i+1,j,time);
AddBee(i,j-1,time); AddBee(i,j+1,time);
}
}
В момент времени time медведь заходит в точку (i,
j). Он может войти в нее, если:
·
она находится в пределах леса;
·
в этой точке находится трава (дом
Миши мы объявили “травой”);
·
в этой точке нет пчел (bees[i][j]
> time);
·
Миша еще не был раньше в этой
точке (mecho[i][j] содержит наименьшее время, за которое медведь
сможет добраться до нее);
Устанавливаем flag = 1, если в какой-то момент
времени Миша достиг дома, имеющего координаты (POS_endX, POS_endY). В
таком случае поиск останавливаем и возвращаемся из функции AddMecho.
void AddMecho(int
i, int j, int
time)
{
if (flag) return;
if ((i <
0) || (j < 0) || (i >= n) || (j >= n)) return;
if
((m[i][j] != 'G') ||
(bees[i][j] <= time)
||
(mecho[i][j] <= time)) return;
DequeX[len] = i;
DequeY[len++] = j;
mecho[i][j] = time;
if ((i ==
POS_endX) && (j == POS_endY)) flag = 1;
}
Моделируем движение медведя поиском в ширину, используя
очередь.
void RunMecho(void)
{
int i, j, k,
time;
for(k = 0; k
< len; k++)
{
i = DequeX[k]; j = DequeY[k]; time =
mecho[i][j] + 1;
AddMecho(i-1,j,time); AddMecho(i+1,j,time);
AddMecho(i,j-1,time); AddMecho(i,j+1,time);
if (flag) return;
}
}
Основная часть программы. Карту леса читаем в символьный
массив m.
memset(bees,0x3F,sizeof(bees));
scanf("%d %d\n",&n,&s);
for(i = 0; i < n; i++) gets(m[i]);
Просматриваем посимвольно карту леса. Ищем начальное
положение медведя (POS_beginX, POS_beginY), координаты дома медведя (POS_endX, POS_endY), а также расположение ульев с пчелами. Поскольку пчелы не
могут залететь в дом Миши, отметим его на карте как “дерево”. Начальное
положение Миши объявим как “трава” (на него могут залететь пчелы).
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
{
if (m[i][j]
== 'M')
{
POS_beginX = i; POS_beginY = j;
m[i][j] = 'G';
} else
if (m[i][j]
== 'D')
{
POS_endX = i; POS_endY = j;
m[i][j] = 'T';
} else
if (m[i][j]
== 'H')
m[i][j] = 'G',
AddBee(i,j,0);
}
Заполняем
массив bees времени распространения пчел по лесу.
FillBees();
Дом медведя теперь меняем с состояния “дерево” на “трава”,
чтобы медведь смог в него попасть (в клетку с деревом медведь зайти не может).
m[POS_endX][POS_endY]
= 'G';
Ищем максимально возможное количество минут на промежутке [Left;
Right], на
протяжении которых Миша может продолжать есть мед в начальном расположении,
имея возможность безопасно вернуться домой. Для этого используем бинарный
поиск.
Left = -1; Right
= bees[POS_beginX][POS_beginY] / s + 1;
while(Left < Right)
{
Mid = (Left + Right + 1) / 2;
Для
значения Mid следует определить, сможет ли медведь есть мед в точности Mid
минут, после чего безопасно вернуться домой.
memset(mecho,0x3F,sizeof(mecho));
Медведь начинает движение из точки (POS_beginX, POS_beginY) в
момент времени Mid * s (через s минут после сигнала
тревоги).
flag = len = 0;
AddMecho(POS_beginX,POS_beginY,Mid*s);
RunMecho();
Отметим, что mecho[i][j] = µ, если медведь не сможет добраться
до точки (i, j) (или его в этой точке ужалят пчелы, или там
находится дерево).
if
(mecho[POS_endX][POS_endY] == 0x3F3F3F3F) Right = Mid - 1;
else Left =
Mid;
}
Выводим ответ.
printf("%d\n",Left);