295. Circle
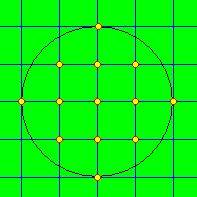
How many points with
integer coordinates are in a circle with radius r? The point on a circle is considered to be in a circle. The
center of the circle has integer coordinates.
Input. The integer radius of a circle r (r ≤ 15000).
Output. Print the required number of points.
|
Sample
input |
Sample
output |
|
2 |
13 |
SOLUTION
loop
Algorithm analysis
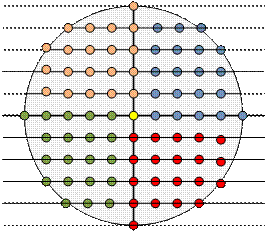
Divide the set
of points with integer coordinates into five parts as shown on the left in the
figure: one point lies in the center, the other four sets are equal to each
other and cover four parts of the circle. If the number of points in the first
quarter is res, then the total number of points in the circle is 4 * res + 1.
To calculate the
value of res, find such a number
of pairs of integers (i, j) that 0 ≤ i ≤
r and 1 ≤ j
≤ r. This can be done with a nested loop in O(r2).
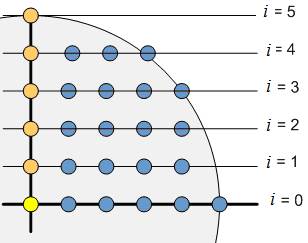
Consider an
algorithm for finding res in O(r).
The axis y = k (0 ≤ k ≤ r) inside the circle contains exactly ![]() integer points. Therefore, the total
number of points res in the first quarter is
integer points. Therefore, the total
number of points res in the first quarter is
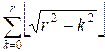
Algorithm realization – O(r2)
Read the radius
of a circle r.
res = 0;
scanf("%d",&r);
Count the number of integer points in the first quarter.
for(i = 0; i <= r; i++)
for(j = 1; j <= r; j++)
if(i*i + j*j <= r*r) res++;
Print the answer.
printf("%d\n",res
* 4 + 1);
Algorithm realization – O(r)
#include <stdio.h>
#include <math.h>
int r, y, res;
double r2;
int main(void)
{
scanf("%d",&r);
res = 0; r2 = r*r;
for(y = 0; y <= r; y++)
res += (int)sqrt(r2 - y*y);
res = 4 * res + 1;
printf("%d\n",res);
return 0;
}
Java realization – O(r2)
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int r = con.nextInt();
int res = 0;
for(int i = 0; i <= r; i++)
for(int j = 1; j <= r; j++)
if(i * i + j * j <= r * r) res++;
System.out.println(res * 4 +
1);
con.close();
}
}
Java realization – O(r)
import java.util.*;
public class Main
{
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
int r = con.nextInt();
int res = 0, r2 = r*r;
for(int y = 0; y <= r; y++)
res += (int)Math.sqrt(r2 - y*y);
res = 4 * res + 1;
System.out.println(res);
con.close();
}
}
Python realization – O(r2)
r = int(input())
res = 0
for i in range(r+1):
for j in range(1,r + 1):
if i * i + j * j <= r
* r: res += 1
res = res * 4 + 1
print(res)
Python realization – O(r)
import math
r = int(input())
res = 0
r2 = r*r
for y in range(r + 1):
res += (int)(math.sqrt(r2 -
y*y))
res = res * 4 + 1
print(res)